|
《人造卫星》讲与练 陕西省宝鸡市陈仓区教育局教研室 邢彦君 一、内容 1．卫星的环绕运动轨道 人造地球卫星的轨道分赤道轨道、极地轨道和倾斜轨道三种。赤道轨道平面与地球的赤道平面重合，地球同步通讯卫星的轨道就是赤道轨道。极地轨道通过地球的两极，军事侦查、资源探测卫星的轨道是极地轨道。不管哪种轨道，其轨道的圆心都必须与地心重合。 2．卫星的环绕运动 利用火箭或航天飞机，将卫星送到预定轨道后，使卫星获得沿轨道切线方向的速度，并使速度与轨道半径之间满足关系  ，即 ，卫星便在距地面h高度处的轨道上以速度v匀速圆周运动。3．卫星的发射与回收 （1）人造地球卫星的发射与回收：在地面上发射人造卫星，一般先是将卫星送到距离地面较近的停泊轨道做圆周运动，再使卫星突然加速，脱离原来的轨道做椭圆运动，此时地球处在椭圆的一个焦点上。当卫星经过椭圆轨道的远地点时，使其突然加速，卫星将在以远地点到地球的距离为半径的圆周上做圆周运动。对于在工作轨道上圆周运动的卫星，若使其突然减速，则将做椭圆轨道运动，当卫星经过近地点时再减速，卫星将在更小的椭圆轨道运动，通过多次减速，卫星将落向地球。 （2）从地球上发射月球（外星）的卫星：先让其绕地球运动，然后实施一系列的加速变轨，逐渐增大椭圆轨道的半长轴，使椭圆轨道逐渐接近月球（称为奔月轨道或地月转移轨道），当月球对卫星的引力远大于地球引力后，卫星将被月球俘获，在较大的椭圆轨道绕月运动。接着实施一系列的减速（制动）变轨，将逐渐减小卫星的轨道半径，使卫星在较小的椭圆或圆轨道上实施探月工作。 4．三个宇宙速度：  km/s称为第一宇宙速度，是人造地球卫星环绕地球做圆周运动的最大线速度，对应的轨道半径等于地球半径； km/s称为第二宇宙速度，是指在地球上发射的人造天体，脱离地球引力束缚，环绕太阳运动的最小速度； km/s称为第三宇宙速度，是指在地球上发射的人造天体，脱离太阳引力束缚，脱离太阳系的最小速度。二、重难点 1．卫星的圆周运动：对卫星的圆周运动，由基本关系可知，  ， 、 、 。因此可知，对于卫星的圆周运动，轨道半径决定一切。2．卫星的变轨运动：做圆周运动的卫星，若被突然加速或减速，则将脱离原轨道，在较大或较小轨道做椭圆轨道运动，地球处在椭圆的一个焦点上。 3．第一宇宙速度的推导：对于近地卫星环绕地球的圆周运动，由  及 得： 。代入地球半径R=6.4 106m、地面的重力加速度g=9.8m/s可得：v=7.9km/s。三、易混点 1．人造天体的发射速度对轨道的影响：在地面发射人造天体，若它获得的切向速度大于第一宇宙速度小于第二宇宙速度，则它做椭圆轨道运动，地球在轨道的一个焦点上，速度越大，轨道的半长轴越大；若获得的切向速度大于第一宇宙速度小于第二宇宙速度，它将绕太阳做椭圆轨道运动，太阳在轨道的一个焦点上，速度越大，椭圆的半长轴越大；若获得的切向速度大于第三宇宙速度，它将受到时太阳引力的束缚，不绕太阳运动。 2．近地卫星与同步卫星：近地卫星是指轨道半径等于地球半径的卫星，通常将离地面高度远小于地球半径的卫星视为近地卫星，它的加速度、速度是所有地球卫星中最大的，它的周期是所有卫星中最小的，约为84分针。因此，人类不可能发射周期小于84分针的人造卫星。同步卫星是指与地球自转同步，即相对地面静止的人造卫星，其周期等于地球的自转周期，轨道都在赤道上方。由 可知，所有地球同步卫星的轨道半径相等。所以，所有的同步卫星，都在同一轨道上以相同的速度运动着。四、题型与方法 1．对于卫星的圆周运动，一般运用基本关系和“黄金代换”分析求解；对于卫星的椭圆轨道运动，一般可运用开普勒定律分析求解其速度的变化，运用牛顿第二定律及万有引力定律分析求解其引力及加速度的变化。 2．对于环绕同一天体的几个卫星，一般可运用开普勒第三定律，分析求解其周期与轨道半径的关系。两个卫星与在中心天体同侧测共线时，相距最近；在中心天体异侧共线时，相距最远。从某次相距最近（最远）到下次最近（最远），内侧卫星比外侧卫星多转一圈，从某次相距最近（最远）到下次最远（最近），内侧卫星比外侧卫星多转半圈。 例1．质量为m的探月航天器在接近月球表面的轨道上飞行，其运动视为匀速圆周运动。已知月球质量为M，月球半径为R，月球表面重力加速度为g，引力常量为G，不考虑月球自转的影响，则航天器的 A．线速度  B．角速度 C．运行周期  D．向心加速度 解析：对航天器环绕月球的圆周运动有： 、 、 、 。解得：， ， ， 。由于，所以又有： ，。本题选AC。例2．某颗地球同步卫星正下方的地球表面上有一观察者，他用天文望远镜观察被太阳照射的此卫星。试问春分那天（太阳光直射赤道）在日落后12小时内有多长时间该观察者看不见此卫星？已知地球半径为R，地球表面处的重力加速度为g，地球自转周期为T，不考虑大气对光的折射。 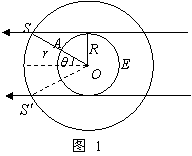  解析：如图1所示，E为地球赤道，S表示卫星，A表示观察者，O表示地心。由图可知春分那天日落后，当卫星由位置S运动到  位置过程中，恰好处于地球的阴影区域，卫星无法反射阳光，观察者看不到卫星。设地球质量、卫星质量分别为M、m，卫星轨道及地球半径分别为r、R，由万有引力定律及牛顿第二定律有： ，由几何关系有： 。观察者观察不到卫星的时间为： ，在地球表面有： 。解得： 。例2．如图2所示，A是地球的同步卫星。另一卫星B的圆形轨道位于赤道平面内，离地面高度为h。已知地球半径为R，地球自转角速度为ωo，地球表面的重力加速度为g，O为地球中心。 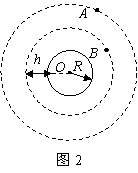  （1）求卫星B的运行周期。 （2）如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近（O、B、A在同一直线上），则至少经过多长时间，它们再一次相距最近？ 解析：（1）对卫星B绕地球的运行，由万有引力定律和牛顿第二定律有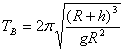：  ，在地面有： ，解得： 。（2）两卫星从本次最近到下次最近，B比A多运动一周，故有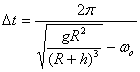：  ，而 ，由于卫星A是同步卫星， ，解得： 。五、强化训练 1．如图3所示，“东方红一号”卫星的运行轨道为椭圆轨道，其近地点M和远地点N的高度分别为439km和2384km，则 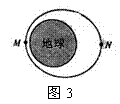  A．卫星在M点的势能大于N点的势能 B．卫星在M点的角速度大于N点的角速度 C．卫星在M点的加速度大于N点的加速度 D．卫星在N点的速度大于7.9km/s 2．在地球（看作质量均匀分布的球体）上空有许多同步卫星，下面说法中正确的是 A．它们的质量可能不同 B．它们的速度可能不同 C．它们的向心加速度可能不同 D．它们离地心的距离可能不同 3．如图4所示，飞船先沿椭圆轨道飞行，后在远地点343千米处点火加速，由椭圆轨道变成高度为343千米的圆轨道，在此圆轨道上飞船运行周期约为90分钟。下列判断正确的是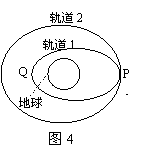：   A．飞船在变轨前后的机械能相等 B．飞船在圆轨道上时航天员出舱前后都处于失重状态 C．飞船在圆轨道上运动的角速度大于同步卫星运动的角速度 D．飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度 强化训练参考答案与解析 1．BC 解析：卫星由M点运动到N点，地球对它的引力做负功，势能增加，动能减小，线速度减小，角速度减小；卫星在M点所受万有引力（合力）大于N点，在M点的加速度大于N点；卫星在N点时离地心的距离大于地球半径，速度小于近地卫星环绕速度（第一宇宙速度）。 2．A 解析：同步卫星的运动周期对等于地球自转周期To，设地球质量为M、卫星到地心的距离（轨道半径）为r，卫星质量为m，对它们环绕地球的运动，由万有引力定律及牛顿第二定律有：  。解得： ，由此可知，所有同步卫星离地心的距离相等，与卫星质量无关，即所有的同步卫星都在同一轨道上运动。因此，它们的向心加速度、线速度、角速度都相同。3．BC 解析：由于飞船发动机做功，飞船点火变轨前后的机械能不守恒；航天员出舱前后都处于失重状态；飞船在圆轨道上运动的周期90分钟小于同步卫星运动的周期24小时，根据  可知，飞船在圆轨道上运动的角速度大于同步卫星运动的角速度；飞船变轨前通后过椭圆轨道远地点时，两次万有引力（合力）相等，加速度相等。
(责任编辑：admin) |