|
绳、杆相关联物体的速度求解 江苏省新沂市第一中学 张统勋 绳、杆等有长度的物体，在运动过程中，如果两端点的速度方向不在绳、杆所在直线上，两端的速度通常是不一样的，但两端点的速度是有联系的，称之为“关联”速度。 “关联速度”问题特点：沿杆或绳方向的速度分量大小相等。 绳或杆连体速度关系：①由于绳或杆具有不可伸缩的特点，则拉动绳或杆的速度等于绳或杆拉物的速度。②在绳或杆连体中，物体实际运动方向就是合速度的方向。③当物体实际运动方向与绳或杆成一定夹角时，可将合速度分解为沿绳或杆方向和垂直于绳或杆方向的两个分速度。 常用的解题思路和方法：先确定合运动的方向，即物体实际运动的方向，然后分析这个合运动所产生的实际效果，即一方面使绳或杆伸缩的效果；另一方面使绳或杆转动的效果。以确定两个分速度的方向，沿绳或杆方向的分速度和垂直绳或杆方向的分速度，而沿绳或杆方向的分速度大小相同。 一、绳相关联问题 1．一绳一物题型 ⑴所拉的物体匀速运动 【例1】如图1所示, 人在岸上拉船，已知船的质量为m，水的阻力恒为f，当轻绳与水平面的夹角为θ时，船的速度为v，此时人的拉力大小为T，则此时 A．人拉绳行走的速度为vcosθ B．人拉绳行走的速度为v/cosθ C．船的加速度为 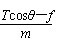 D．船的加速度为 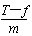 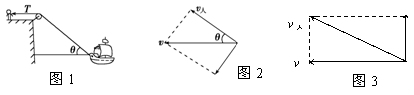 解析：船的速度产生了两个效果: 一是滑轮与船间的绳缩短, 二是绳绕滑轮顺时针转动, 因此将船的速度进行分解如图所示, 人拉绳行走的速度v人=vcosθ, A对, B错；绳对船的拉力等于人拉绳的力，即绳的拉力大小为T，与水平方向成θ角，因此Tcosθ-f＝ma，解得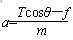：  ，C正确，D错误。答案：AC。 点评：人拉绳行走的速度即绳的速度，易错误地采用力的分解法则，将人拉绳行走的速度。即若按图3所示进行分解，则水平分速度为船的速度，得人拉绳行走的速度为v/cosθ，会错选B选项。 ⑵匀速拉动物体 【例2】如图4所示，在河岸上利用定滑轮拉绳索使小船靠岸，拉绳的速度为v，当拉船头的绳索与水平面的夹角为α时，船的速度是多少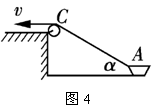？  解析：方法1——微元分析法  取小量θ，如图5所示，设角度变化θ所需的时间为Δt，取CD=CB，在Δt时间内船的位移为AB，绳子端点C的位移大小为绳子缩短的长度AD。由于θ→0°，所以∠BDA→90°。所以AD=ABcosα ① 又AD=vΔt ② AB=v船Δt ③ 由上述三式可得：v船=v/cosα 方法2——运动等效法 因为定滑轮右边的绳子既要缩短又要偏转，所以定滑轮右边绳上的A点的运动情况可以等效为：先以滑轮为圆心，以AC为半径做圆周运动到达B，再沿BC直线运动到D。做圆周运动就有垂直绳子方向的线速度，做直线运动就有沿着绳子方向的速度，也就是说船的速度(即绳上A点的速度)的两个分速度方向是：一个沿绳缩短的方向，另一个垂直绳的方向。作矢量三角形如图6所示，v船＝v/cosα。 点拨：方法1利用几何知识构建三角形，找出在Δt时间内绳与船的位移关系，进而确定速度关系；方法2利用了实际运动为合运动，按效果对船的速度进行分解。 2．两绳一物题型 【例3】如图7所示，两绳通过等高的定滑轮共同对称地系住一个物体A，两边以v速度匀速地向下拉绳。当两根细绳与竖直方向的夹角都为60°时，物体A上升的速度多大？   解析：以右边绳子为研究对象，应用绳连体模型的结论，当绳端物体A在做既不沿绳方向，又不垂直于绳方向运动时，一般要将绳物体A的真实运动分解到沿绳收缩方向和垂直于绳子方向的两个分运动。其运动效果一是沿绳方向的直线运动，这使得绳变短，二是以定滑轮为圆心的圆周运动，这使得绳转过了一个小角度，即A的运动就是这两个分运动的合成。如图8所示，有  ，则 。点评：本题是一道绳连体的速度问题，有部分学生认为物体A参与两边绳子的分运动，物体A上升的速度为合速度，容易错解成  ，等同于力的合成与分解。3．一绳两物题型 ⑴水平方向情况分析 【例4】A、B两物体通过一根跨过定滑轮的轻绳相连放在水平面上，现物体A以v1的速度向右匀速运动，当绳被拉成与水平面夹角分别是α、β时，如图9所示。物体B的运动速度vB为（绳始终有拉力）   A．  B． C． D． 解析：A、B两物体通过绳相连接，且两物体都是运动的，物体的实际运动速度是合速度，物体的速度都产生了沿绳方向和垂直于绳方向两个作用效果。设物体B的运动速度为vB，此速度为物体B合运动的速度，根据它的实际运动效果，两分运动分别为：沿绳收缩方向的分运动，设其速度为v绳B；垂直绳方向的圆周运动，速度分解如图10所示，则有vB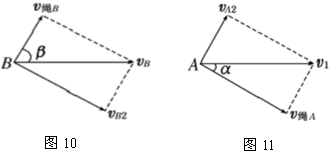＝  ①  物体A的合运动对应的速度为v1，它也产生两个分运动效果，分别是：沿绳伸长方向的分运动，设其速度为v绳A；垂直绳方向的圆周运动，它的速度分解如图11所示，则有v绳A=v1cosα ② 由于对应同一根绳，其长度不变，故v绳B=v绳A ③ 根据三式解得：vB＝ 。选项ABC错误D正确。答案：D 点评：此题涉及多个物体的速度分解，应用隔离法将每个物体的速度进行分解，再通过关联速度进行求解。 ⑵竖直方向情况分析 【例5】如图12所示，竖直平面内放置一直角杆AOB，杆的水平部分粗糙，竖直部分光滑，两部分各有质量相等的小球A和B套在杆上，A、B间用轻绳相连，以下说法中正确的是 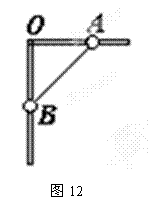  A．若用水平拉力向右缓慢地拉A，则拉动过程中A受到的摩擦力不变 B．若以一较明显的速度向右匀速地拉A，则拉动过程中A受到的摩擦力不变 C．若以一较明显的速度向右匀速地拉A，则过程中A受到的摩擦力比静止时的摩擦力要大 D．若以一较明显的速度向下匀速地拉B，则过程中A受到的摩擦力与静止时的摩擦力相等 解析：当A滑动时，A受到的摩擦力是滑动摩擦力，在动摩擦因数不变的情况下，其大小只与正压力有关。若用水平拉力向右缓慢地拉A，两小球都处于平衡状态，选取两球组成的系统为研究对象，该系统在竖直方向上受到总重力和水平杆对A球竖直向上的支持力N的作用，二力平衡，所以 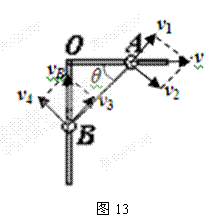 ，可见，支持力N不变，又因为A受到的摩擦力 ，所以 不变，选项A正确。若用水平拉力向右以一较明显的速度向右匀速地拉A，则两球实际运动的速度可以看作合速度，它们均可以分解为沿绳方向的分速度和垂直绳方向的分速度，并且两球沿绳方向的分速度大小相等，设A球匀速运动的速度为v，轻绳AB与水平杆间的夹角为 ，如图13所示，则 ， ， ，所以 ，可见，当A球向右运动时，变大， 也变大，即B球在竖直方向上做加速运动，所以轻绳对B球拉力的竖直向上的分量大于GB，根据牛顿第三定律，轻绳对A球竖直向下的拉力分量也大于GB，所以N=GA＋GB，A受到的摩擦力> ，选项B错误，C正确；若以一较明显的速度向下匀速地拉B，那么由两球组成的系统在竖直方向上受力平衡，则水平杆对A球的弹力N=GA＋GB＋F，其中F为拉力，可见N比静止时要大，所以该过程中A受到的摩擦力经静止时大，选项D错误。  答案：AC 点评：竖直方向的物体分析，涉及到超、失重情况，分析时应加以注意，否则易出现错误。 二、杆相关联问题 【例6】如图14所示，一根长直轻杆AB在墙角沿竖直墙和水平地面滑动，当AB杆和墙的夹角为θ时，杆的A端沿墙下滑的速度大小为v1，B端沿地面的速度大小为v2。则v1、v2的关系是( ) 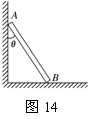  A．v1＝v2 B．v1＝v2cosθ C．v1＝v2tanθ D．v1＝v2sinθ 解析：如图15所示，轻杆A端下滑速度v1可分解为沿杆方向的速度v1′和垂直于杆的方向速度v1″，B端水平速度v2可分解为沿杆方向的速度v2′和垂直于杆的方向速度v2″，由于沿杆方向的速度相等v1′＝v2′，由数学知识可知，v1′＝v1cosθ，v2′＝v2sinθ，v1＝v2tanθ。故C项正确。 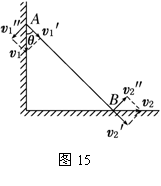  答案：C 点评：对于直杆的运动，一般将其两端的运动速度沿杆和垂直于杆的两个方向分解，两端速度沿杆的分量相等。 (责任编辑：admin) |