|
寻找向心力 陕西省宝鸡市陈仓区教育局教研室 邢彦君 匀速圆周运动是变速运动，运动中质点始终具有指向轨道圆心的加速度——向心加速度，由牛顿第二定律可知，物体始终受到指向轨道圆心的合力——向心力。对匀速圆周运动的物体，运用牛顿第二定律可分析求解某状态时的力、速度或轨道半径，分析求解的关键是寻找质点所受的向心力。 向心力是效果力，它可以是某一个力，也可以是几个力的合力。在匀速圆周运动中，它的方向总是指向轨迹的圆心；在竖直平面上的非匀速圆周运动中，当质点经过轨道的最高点及最低点时，合力的方向也指向轨迹圆心。 1．弹力提供向心力 连接在绳、杆或弹簧一端的物体，绕绳、杆或弹簧另一端在水平平面做匀速圆周运动时，绳、杆或弹簧由于弹性形变而产生弹力，弹力提供物体圆周运动的向心力；附着在绕竖直轴匀速转动的圆通内壁，随圆通内壁匀速圆周运动的物体，与圆通内壁相互挤压，圆通内壁产生弹力，弹力提供物体匀速圆周运动的向心力。 例1．如图1所示，在光滑水平桌面上有一光滑小孔O。一根轻绳穿过小孔，一端连接质量为m=1kg的小球A，另一端连接质量为M=4kg的物体B。 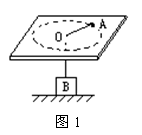 （1）小球A沿半径r=0.1m的圆周做匀速圆周运动，角速度为ω=10rad/s。物体B对地面的压力为多大？ （2）当小球A的角速度为多大时，物体B处于将要离开、而尚未离开地面的临界状态？（g=10m/s2） 解析：由于小孔O光滑，因此，轻绳对小球A及物体B的拉力大小相等，对小球A的拉力沿水平方向指向O，对物体B的拉力竖直向上。 （1）设轻绳的拉力为T，地面对物体B的支持力为N。对水平面上匀速圆周运动的小球A运用牛顿第二定律有：  ；对静止于地面的物体B运用共点力平衡条件有： 。代入数据解得：N=30N。由牛顿第三定律可知，物体B对地面的压力大小是30N，方向竖直向下。（2）当物体B处于将要离开、而尚未离开地面的临界状态时，地面对它的支持力等于零。因此，令N=0，解 和可得：ω=20rad/s。所以，当小球A的角速度为ω=20rad/s时，物体B处于将要离开、而尚未离开地面的临界状态。2．静摩擦力提供向心力 物体在水平面做圆周运动，由于有沿半径向外的运动趋势，它会受到水平面对它沿半径向内的静摩擦力作用，静摩擦力提供物体做圆周运动的向心力。如物体在水平圆盘上随盘的转动，汽车在水平地面上的转弯等。 例2．质量为4000kg的汽车在水平地面行驶，地面对汽车的最大静摩擦力为16000N。将汽车转弯时运动视为匀速圆周运动，则： （1）若汽车保持20m/s的速率转弯，则最小转弯半径是多少？ （2）若汽车以9m的转弯半径转弯，则最大转弯速率是多少？ 解析：汽车在水平地面转弯，转弯时汽车的运动可视为匀速圆周运动，所需向心力由地面对汽车的静摩擦力提供。 （1）在转弯速率一定时，转弯半径越小，所需向心力越大，而地面所能还提供的最大向心力就是地面对汽车的最大静摩擦力，对汽车的转弯运动运用牛顿第二定律有：  ，代入数据解得最小转弯半径为：r=10m。（2）在转弯半径一定时，汽车的速率越大，所需向心力越大，而地面所能还提供的最大向心力就是地面对汽车的最大静摩擦力。对汽车的转弯运动运用牛顿第二定律有： ，代入数据解得汽车转弯的最大速率为：v=6m/s。3．几个力的合力提供向心力 物体匀速圆周运动时，所受各力的方向均不在或部分力的方向不在圆周运动轨道平面上时，各力的合力提供圆周运动的向心力。 例3．有一种叫“飞椅”的游乐项目，示意图如图2所示，长为L的钢绳一端系着座椅，另一端固定在半径为r的水平转盘边缘。转盘可绕穿过其中心的竖直轴转动。当转盘以角速度ω匀速转动时，钢绳与转轴在同一竖直平面内，与竖直方向的夹角为θ。不计钢绳的重力，求转盘转动的角速度ω与夹角θ的关系。 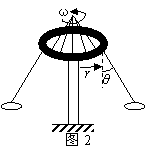  解析：当转盘以角速度ω匀速转动时，座椅以角速度ω在水平面上做匀速圆周运动，此时座椅受沿钢丝绳斜向上的拉力T和竖直向下的重力作用，如图3所示。由几何关系可知，座椅匀速圆周运动的轨道半径为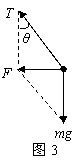：  。对座椅的匀速圆周运动运用牛顿第二定律有： 。依据图3，由平行四边形定则有： 。解此两式得，转盘转动的角速度ω与夹角θ的关系为： 。  例4．质量为m的汽车，在行驶途中将经过半径为R的景观凸拱桥。若此拱桥能承受的最大压力为No（  ），求汽车能安全经过此桥的速度范围。解析：欲使汽车安全过桥，汽车经过桥的最高点时不能飞离桥面，也不能将桥压坏，即汽车对桥面的最大压力不能超过桥面所能承受的最大压力No，也不能等于零。设汽车以速度v经过桥面上某位置，如图4所示，对汽车经过该位置的运动在径向运用牛顿第二定律有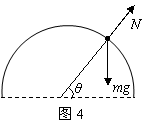：  。由此式可知，在汽车质量m、桥面半径R、行驶速度v一定时， 时，即汽车经过桥面最高点时，对桥面的压力最大。所以，只要汽车经过最高点时不将桥面压坏，则经过其它位置时不会将桥面压坏。  汽车经过桥的最高点时，对其运用牛顿第二定律有：  。当汽车将要离开桥面时，对桥面的压力为零，令N=0，解得： ；令N=No，解得： 。所以，汽车能安全经过此桥的速度范围为： 。
(责任编辑：admin) |