|
《万有引力定律的成就》讲与练 陕西省宝鸡市陈仓区教育局教研室 邢彦君 一、内容 1.计算天体的质量 (1)利用围绕某天体圆周运动的天体的轨道半径r、运动周期T,由关系式 (2)利用测得的某天体表面的重力加速度g、天体的半径R, 由关系式 2.计算天体运动的加速度、速度、及周期 (1)已知中心天体的质量M,环绕运动天体的轨道半径r,由关系式 (2)已知中心天体表面的重力加速度g,半径R,运动天体的轨道半径r,由上述基本关系式及“黄金代换”关系,也可计算运动天体的加速度、线速度、角速度及周期。 3.发现“未知”天体:如果某天体环绕运动过程中,在某区域,轨道偏离原轨道,说明此区域存在尚未观测到的天体,依据轨道的偏离情况,运用万有引力定律及其它力学规律,可测算出“未知”天体的位置、质量等。 二、重难点 1.分析求解天体运动问题时,将运动天体与中心天体视为质点,天体的环绕运动是匀速圆周运动,中心天体对运动天体的万有引力充当向心力,不考虑中心天体以外的其它天体的万有引力。 2.对于人造天体的圆周运动,它运动的加速度、线速度、角速度、周期,受轨道半径的制约,轨道半径变化,这些量随之改变。 三、易混点 1.中心天体与环绕运动天体:利用基本关系式,只能计算出处在轨道中心的中心天体的质量,无法计算出环绕运动天体的质量。 2.公转周期与自转周期:利用基本关系 3.圆周运动与双星运动:两颗相距较近的天体,其中的一天体不环绕另一天体运动,两者共同环绕其内侧连线上某一点做圆周运动,运动中两天体的轨道是同心圆。若两天体的质量悬殊,则它们运动的公共圆心离质量较大的天体很近,此时的双星运动可视为小质量天体环绕大质量天体的圆周运动。 4.“黑洞”与天体:“黑洞”是指质量或密度非常大的天体,其它天体可以环绕其运动,它也可以环绕其它天体运动,它也可与其它天体形成双星。 四、题型与方法 1.对于环绕运动,分析求解的基本思路与方法,就是万有引力定律、牛顿第二定律、匀速圆周运动规律的综合运用。可视问题情境灵活选用 2.对于有自转的天体,其上各部分物体随天体的自转做圆周运动,不同纬度处的同质量物体,圆周运动的轨道半径不同,赤道上的物体自转的轨道半径最大,所需向心力最大。当赤道上物体恰要被甩出时,它与天体表面的作用力为零,只是万有引力充当向心力。由 3.双星运动中的相等量:双星运动中,两天体的向心力相等,角速度相等,周期相等。 例1.开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即 (1)请你推导出太阳系中该常量k的表达式。 (2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106s,试计算地球的质M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字) 解析:(1)因行星绕太阳作匀速圆周运动,于是轨道的半长轴a即为轨道半径r。由万有引力定律和牛顿第二定律有: (2)在月地系统中,设月球绕地球运动的轨道半径为R,周期为T,对月球绕地球的运动,由上述结论有: 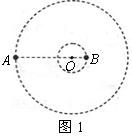 例2.如图1所示,质量分别为m和M的两个星球A和B在彼此引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。 例2.如图1所示,质量分别为m和M的两个星球A和B在彼此引力作用下都绕O点做匀速周运动,星球A和B两者中心之间距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。(1)求两星球做圆周运动的周期; (2)在地月系统中,若忽略其它星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行为的周期记为T1。但在近似处理问题时,常认为月球是绕地心做圆周运动的,这样算得的运行周期T2。已知地球和月球的质量分别为5.98×1024kg 和 7.35 ×1022kg 。求T2与T1两者平方之比。(结果保留3位小数) 解析:(1)A和B绕O做匀速圆周运动,它们之间的万有引力提供向心力,则A和B的向心力相等。且A和B和O始终共线,则 A和B有相同的角速度或周期。因此有: 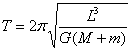 。 。(2)将地月看成双星,则  。将月球看作绕地心做圆周运动,由牛顿第二定律和万有引力定律有: 。将月球看作绕地心做圆周运动,由牛顿第二定律和万有引力定律有:例2.中子星是恒星演化过程的一种可能结果,它的密度很大。现有一中子星,观测到它的自转周期为 解析:设中子星的质量为M,赤道半径是R,对于中子星赤道上质量为m的部分物质,有关系式: 五、强化训练 1.一物体静置在平均密度为 A. 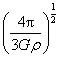 B. B.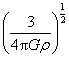 C. C.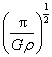 D. D.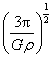 2.火星探测项目是我国继神舟载人航天工程、嫦娥探月工程之后又一个重大太空探索项目。假设火星探测器在火星表面附近圆轨道运行的周期为 A. 3.冥王星与其附近的另一星体卡戎可视为双星系统,质量比约为7∶1,同时绕它们连线上某点O做匀速圆周运动,由此可知,冥王星绕O点运动的 A.轨道半径约为卡戎的 C.线速度大小约为卡戎的7倍速 D.向心力大小约为卡戎的7倍 强化训练参考答案与练习 1.D 解析:由 2.D 解析:对火星探测器的环绕运动有: 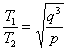 。本题选D。 。本题选D。3.A 解析:双星系统中两天体在彼此之间的万有引力作用下做匀速圆周运动,所以向心力,角速度,周期均相等;由有基本关系 |
