《3.2 古典概型》测试题
一、选择题
1.将骰子向桌面上先后抛掷2次,其中向上的点数之积为12的结果有( ).
A.2种 B.4种 C.6种 D.8种
考察目的:考查古典概型的意义,了解古典概型同每个基本事件出现的可能性相等.
答案:B.
解析:将骰子向桌面上先后抛掷2次,其中向上的点数之积为12的结果有(3,4),(4,3),(2,6),(6,2).
2.(2012·安徽文)袋中共有6个除了颜色外完全相同的球,其中有1个红球,2个白球和3个黑球,从袋中任取两球,两球颜色为一白一黑的概率等于( ).
A.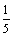 B. B. C. C.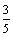 D. D.
考查目的:考查用列举法计算随机事件的基本事件数及事件发生的概率.
答案:B.
解析:1个红球,2个白球和3个黑球分别记为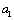 , ,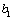 , ,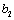 , ,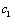 , , , ,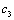 ,从袋中任取两球共有15种,列举如下: ,从袋中任取两球共有15种,列举如下: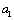 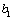 , ,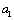 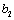 , ,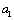 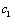 , ,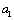  , ,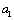 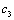 , ,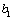 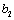 , ,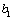 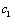 , ,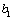  , ,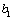 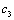 , ,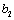 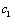 , ,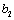  , ,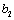 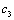 , ,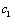  , ,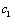 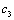 , , 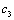 ,满足两球颜色为一白一黑有6种,概率等于 ,满足两球颜色为一白一黑有6种,概率等于 . .
3.(2011·安徽文) 从正六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于( ).
A.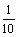 B. B. C. C.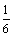 D. D.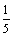
考查目的:考查用列举法求随机事件所含基本事件数及计算古典概型的概率.
答案:D.

解析:正六边形的6个顶点分别用字母A,B,C,D,E,F表示,如图.从6个顶点中随机选择4个顶点,以它们作为顶点的四边形共有15个,列举如下:ABCD,ABCE,ABCF,ABDE,ABDF,ABEF,ACDE,ACDF,ACEF,ADEF,BCDE,BCDF,BCEF,BDEF,CDEF,其中能构成矩形的是ABDE,BCEF,ACDF三种,故概率等于 .(本题也可以画树状图) .(本题也可以画树状图)
二、填空题
4.(2011·江苏)从1,2,3,4这四个数中一次随机取两个数,则其中一个数是另一个的两倍的概率是 .
考查目的:考查古典概型的概率计算公式 . .
答案: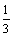 . .
解析:从1,2,3,4这四个数中一次随机取两个数,所有可能的取法有6种:(1,2),(1,3),(1,4),(2,3),(2,4),(3,4),满足“其中一个数是另一个的两倍”的所有可能的结果有(1,2),(2,4)共2种取法,所以其中一个数是另一个的两倍的概率是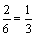 . .
5.(2012·上海春)某校要从2名男生和4名女生中选出4人担任某游泳赛事的志愿者工作,则在选出的志愿者中,男、女都有的概率为_ (结果用数值表示).
考查目的:考查古典概型的概率计算公式和对立事件的概率公式应用等.
答案: . .
解析:要从2名男生和4名女生中选出4人担任某游泳赛事的志愿者工作,共15种结果.只有2名女生,选出的4人中不可能都是女生,所以有2种结果:选出的志愿者中,男、女都有或只有男生,故选出的4人中有可能都是男生且发生的概率为 ,而选出的志愿者中,男、女都有的概率为 ,而选出的志愿者中,男、女都有的概率为 . .
6.(2012·江苏)现有10个数,它们能构成一个以1为首项,-3为公比的等比数列,若从这10个数中随机抽取一个数,则它小于8的概率是 .
考查目的:考查古典概型的概率公式与等比数列知识的综合运用.
答案: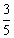 . .
解析:因为以1为首项,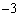 为公比的等比数列的10个数分别为1,-3,9,-27,…,其中有5个负数-3,-27,…,1个正数1,共有6个数小于8,所以从这10个数中随机抽取一个数,它小于8的概率是 为公比的等比数列的10个数分别为1,-3,9,-27,…,其中有5个负数-3,-27,…,1个正数1,共有6个数小于8,所以从这10个数中随机抽取一个数,它小于8的概率是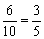 . .
三、解答题
7.(2012·北京理)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
|
“厨余垃圾”箱
|
“可回收物”箱
|
“其他垃圾”箱
|
厨余垃圾
|
400
|
100
|
100
|
可回收物
|
30
|
240
|
30
|
其他垃圾
|
20
|
20
|
60
|
⑴试估计厨余垃圾投放正确的概率;
⑵试估计生活垃圾投放错误的概率;
⑶假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为 ,其中 ,其中 , , .当数据 .当数据 的方差 的方差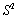 最大时,写出 最大时,写出 的值(结论不要求证明),并求此时 的值(结论不要求证明),并求此时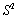 的值.(注:方差 的值.(注:方差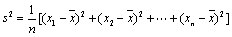 ,其中 ,其中 为 为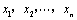 的平均数) 的平均数)
考查目的:考查利用古典概型概率计算公式解决实际问题的能力.
答案:⑴ ;⑵ ;⑵ ;⑶ ;⑶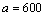 , , , , , ,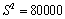 . .
解析:此题的难度集中在第三问,其他两问难度不大,第三问是对能力的考查,不要求证明,即不要求说明理由,但是要求学生对方差意义的理解非常深刻.
⑴由题意可知,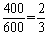 ; ;
⑵由题意可知,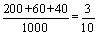 ; ;
⑶由题意可知,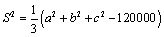 ,因此当 ,因此当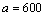 , , , , 时,有 时,有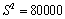 . .
8.(2011·山东文)甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
⑴若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
⑵若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
考查目的:理解古典概型概念并熟练运用古典概型概率公式解决概率问题.
答案:⑴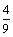 ;⑵ ;⑵ . .
解析:⑴甲校两男教师分别用A、B表示,女教师用C表示;乙校男教师用D表示,两女教师分别用E、F表示.从甲校和乙校报名的教师中各任选1名的所有可能的结果为:(A,D)(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F)共9种.从中选出两名教师性别相同的结果有(A,D),(B,D),(C,E),(C,F)共4种,则选出的两名教师性别相同的概率为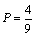 . .
⑵从甲校和乙校报名的教师中任选2名的所有可能的结果为(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种,从中选出两名教师来自同一学校的结果有:(A,B),(A,C),(B,C),(D,E),(D,F),(E,F)共6种,则选出的两名教师来自同一学校的概率为 . .
(责任编辑:admin) |

