|
34．（湖南•理•18题）如图1，  分别是矩形 的边 的中点， 是 上的一点，将 ， 分别沿 翻折成 ， ，并连结 ，使得平面 平面， ，且 ．连结 ，如图2． （I）证明：平面 平面 ；（II）当  ， ， 时，求直线和平面所成的角； 【解答】解法一：（Ｉ）因为平面 平面，平面 平面 ， ， 平面，所以 平面 ，又平面，所以平面 平面．（II）过点  作 于点 ，连结 ．由（I）的结论可知，  平面，所以  是和平面所成的角．因为平面 平面，平面平面 ， ， 平面，所以 平面，故 ．因为 ， ，所以可在上取一点 ，使 ，又因为 ，所以四边形 是矩形．由题设 ，，，则 ．所以 ， ， ， ．因为 平面，，所以 平面，从而 ．故  ， ．又  ，由 得 ．故  ．即直线 与平面所成的角是 ．解法二：（I）因为平面 平面，平面平面，，平面，所以平面，从而 ．又 ，所以平面．因为平面，所以平面平面．（II）由（I）可知， 平面．故可以 为原点，分别以直线 为 轴、 轴、 轴建立空间直角坐标系（如图）， 由题设 ，，，则 ， ， ，相关各点的坐标分别是 ， ， ， ．所以  ， ．设  是平面的一个法向量，由  得 故可取 ．过点  作 平面于点，因为 ，所以 ，于是点在轴上．因为 ，所以 ，．设  （ ），由 ，解得 ，所以  ．设 和平面所成的角是 ，则 ．故直线 与平面所成的角是．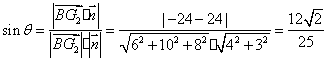35．（江苏•理•18题）如图，已知  是棱长为3的正方体，点在 上，点 在 上，且 。（I）求证：  四点共面；（4分）（II）若点 在 上， ，点 在 上， ，垂足为，求证： 面 ；（Ⅲ）用 表示截面 和面所成锐二面角大小，求 。  【解答】（1）证明：在DD  上取一点N使得DN=1，连接CN，EN，显然四边形CFDN是平行四边形，所以DF//CN，同理四边形DNEA是平行四边形，所以EN//AD，且EN=AD，又BC//AD，且AD=BC，所以EN//BC，EN=BC，所以四边形CNEB是平行四边形，所以CN//BE，所以D F//BE，所以四点共面。（2）因为 所以 ∽ MBG，所以 ，即 ，所以MB=1，因为AE=1，所以四边形ABME是矩形，所以EM⊥BB又平面ABBA⊥平面BCCB，且EM在平面ABBA内，所以面（3） 面，所以BF，MH，，所以∠MHE就是截面和面所成锐二面角的平面角，∠EMH= ，所以 ，ME=AB=3，∽MHB，所以3：MH=BF：1，BF= ，所以MH= ，所以= 36．（江西•理•20题）右图是一个直三棱柱（以A1B1C1为底面）被一平面所截得到的几何体，截面为ABC．已知A1B1＝B1C1＝l，∠AlBlC1＝90°，AAl＝4，BBl＝2，CCl＝3。 （I）设点O是AB的中点，证明：OC∥平面A1B1C1； （II）求二面角B—AC—A1的大小； （Ⅲ）求此几何体的体积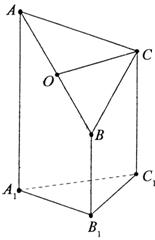；  【解答】解法一： （1）证明：作  交 于 ，连 ．  则  ．因为 是 的中点，所以  ．则  是平行四边形，因此有 ． 平面 且 平面，则  面 ．（2）如图，过 作截面 面，分别交 ， 于 ， ．作  于，连 ．因为  面 ，所以 ，则 平面 ．又因为  ， ， ．所以  ，根据三垂线定理知 ，所以 就是所求二面角的平面角．因为  ，所以 ，故 ，即：所求二面角的大小为  ．（3）因为 ，所以 ． ．所求几何体体积为  ．解法二： （1）如图，以  为原点建立空间直角坐标系，  则  ， ， ，因为是的中点，所以 ， ．易知，  是平面的一个法向量．因为  ，平面，所以平面．（2）  ， ，设  是平面 的一个法向量，则则  ， 得： 取  ， ．显然，  为平面 的一个法向量．则  ，结合图形可知所求二面角为锐角．所以二面角  的大小是．（3）同解法一． (责任编辑：admin) |