|
11、（浙江文）甲、乙两人进行乒乓球比赛，比赛规则为“3局2胜”，即以先赢2局者为胜．根据经验，每局比赛中甲获胜的概率为0．6，则本次比赛甲获胜的概率是 (A1 0．216 (B)0．36 (C)0．432 (D)0．648 【解答】甲获胜有两种情况，一是甲以2：0获胜，此时  二是甲以2：1获胜，此时  ，故甲获胜的概率 【高考考点】独立重复事件恰好发生n次的概率 【易错点】：利用公式  求得答案C,忽视了问题的实际意义。【备考提示】：计算概率问题要仔细分析该事件中所包含的基本事件，分类计算。 12、（浙江文）某校有学生2000人，其中高三学生500人．为了解学生的身体素质情况，采用按年级分层抽样的方法，从该校学生中抽取一个200人的样本．则样本中高三学生的人数为___________．50 【解答】分层抽样即是按比例抽样，易知抽样比例为10：1,故500名高三学生应抽取的人数为50人。 【高考考点】分层抽样的相关知识。 【易错点】：不理解分层抽样的含义或与其它混淆。 【备考提示】：抽样方法是数学中的一个小知识点，但一般不难，故也是一个重要的得分点，不容错过。 13、（上海文）在五个数字  中，若随机取出三个数字，则剩下两个数字都是奇数的概率是 （结果用数值表示）．0.3【解答】剩下两个数字都是奇数，取出的三个数为两偶一奇，所以剩下两个数字都是奇数的概率是  。14、（陕西文）（本小题满分12分）某项选拔共有三轮考核，每轮设有一个问题，能正确回答问题者进入下一轮考试，否则即被淘汰，已知某选手能正确回答第一、二、三轮的问题的概率分别为  、 、 ，且各轮问题能否正确回答互不影响.（Ⅰ）求该选手被淘汰的概率； （Ⅱ）该选手在选拔中回答问题的个数记为ξ，求随机变量ξ的分布列与数数期望.（注：本小题结果可用分数表示） 【解答】解法一：（Ⅰ）记“该选手能正确回答第  轮的问题”的事件为 ，则 ， ， ， 该选手被淘汰的概率  ．（Ⅱ）  的可能值为 ， ， ， ． 的分布列为
 ．解法二：（Ⅰ）记“该选手能正确回答第 轮的问题”的事件为，则，，．该选手被淘汰的概率  ．（Ⅱ）同解法一． 15、（陕西文）某商场有四类食品，其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种，现从中抽取一个容量为20的样本进行食品安全检测。若采用分层抽样的方法抽取样本，则抽取的植物油类与果蔬类食品种数之和是 （A）4 （B）5 （C）6 （D）7 【解答】共有食品100种，抽取容量为20的样本，各抽取  ，故抽取植物油类与果蔬类食品种数之和为2+4=6，选C16、（山东理）某班50名学生在一次百米测试中，成绩全部介于13秒与19秒之间，将测试结果按如下方式分成六组：第一组，成绩大于等于13秒且小于14秒；第二组，成绩大于等于14秒且小于15秒；  第六组，成绩大于等于18秒且小于等于19秒．右图是按上述分组方法得到的频率分布直方图．设成绩小于17秒的学生人数占全班总人数的百分比为 ，成绩大于等于15秒且小于17秒的学生人数为 ，则从频率分布直方图中可分析出和分别为（ ）A．0.9，35 B．0.9，45 C．0.1，35 D．0.1，45 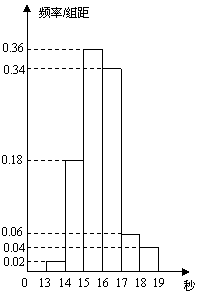  【解答】从频率分布直方图上可以看出  ， .17、（山东理）位于坐标原点的一个质点  按下列规则移动：质点每次移动一个单位；移动的方向为向上或向右，并且向上、向右移动的概率都是 ，质点移动五次后位`于点 的概率是（ ）A．  B． C． D． 【解答】质点在移动过程中向右移动2次向上移动3次，因此质点P 移动5次后位于点  的概率为 。18、（山东理）（本小题满分12分）设  和 分别是先后抛掷一枚骰子得到的点数，用随机变量表示方程 实根的个数（重根按一个计）．（Ⅰ）求方程 有实根的概率；（Ⅱ）求 的分布列和数学期望；（Ⅲ）求在先后两次出现的点数中有5的条件下，方程 有实根的概率．【解答】:（I）基本事件总数为  ，若使方程有实根，则  ，即 。当  时， ；当  时， ；当  时， ；当  时，；当  时， ；当  时，,目标事件个数为  因此方程 有实根的概率为 (II)由题意知，  ，则 ，  ，故 的分布列为
的数学期望 (III)记“先后两次出现的点数中有5”为事件M，“方程  有实根” 为事件N，则 ， ， .19、（山东文）设集合  ，分别从集合 和 中随机取一个数 和，确定平面上的一个点 ，记“点落在直线 上”为事件 ，若事件 的概率最大，则 的所有可能值为（ ）A．3 B．4 C．2和5 D．3和4 【解答】事件 的总事件数为6。只要求出当n=2,3,4,5时的基本事件个数即可。当n=2时，落在直线  上的点为（1，1）；当n=3时，落在直线  上的点为（1,2）、（2,1）；当n=4时，落在直线  上的点为（1,3）、（2,2）；当n=5时，落在直线  上的点为（2,3）；显然当n=3,4时，事件 的概率最大为 。20、（全国II理）在某项测量中，测量结果 服从正态分布 ．若在 内取值的概率为0.4，则在 内取值的概率为 ．0.8【解答】在某项测量中，测量结果x服从正态分布N（1，s2）（s>0），正态分布图象的对称轴为x=1，x在（0，1）内取值的概率为0.4，可知，随机变量ξ在(1，2)内取值的概率于x在(0，1)内取值的概率相同，也为0.4，这样随机变量ξ在(0，2)内取值的概率为0.8。 21、（全国II理）（本小题满分12分）从某批产品中，有放回地抽取产品二次，每次随机抽取1件，假设事件 ：“取出的2件产品中至多有1件是二等品”的概率 ．（1）求从该批产品中任取1件是二等品的概率  ；（2）若该批产品共100件，从中任意抽取2件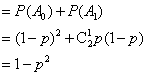， 表示取出的2件产品中二等品的件数，求的分布列．【解答】（1）记  表示事件“取出的2件产品中无二等品”， 表示事件“取出的2件产品中恰有1件二等品”．则  互斥，且 ，故  于是  ．解得  （舍去）．（2） 的可能取值为 ．若该批产品共100件，由（1）知其二等品有  件，故 ． ． ．所以 的分布列为
(责任编辑：admin) |
