江苏省兴化中学 章庭远
在抛物线的教学过程中,不少老师应该遇到过这样一道关于抛物线的焦点弦的题目.
题目:过抛物线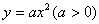 的焦点 的焦点 作直线交抛物线于 作直线交抛物线于 两点,若线段 两点,若线段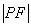 与 与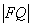 的长度分别为 的长度分别为 则 则 ( ) ( )
A.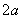 B. B. C. C. D. D.
这道题目有一个快速而且准确的解法,就是我们在解选择题时常用的“特殊值法”或称“特例检验法”.我们可假设直线 与 与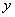 轴垂直,则 轴垂直,则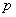 与 与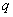 相等,这里还有个特别注意的就是很多学生在解题的时候会犯的一个低级错误,认为抛物线的标准方程中 相等,这里还有个特别注意的就是很多学生在解题的时候会犯的一个低级错误,认为抛物线的标准方程中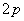 对应的就是 对应的就是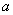 ,其实这里我们要稍微转化一下,本题中与 ,其实这里我们要稍微转化一下,本题中与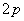 对应的应该是 对应的应该是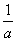 ,故本题答案是 ,故本题答案是 而不是 而不是
但是我们作为老师,不是解完这道题目就了了,我们还可以再仔细分析一下本题,这题很有意思,四个选择支全是常数,也就是说抛物线的焦点弦被焦点分成两部分的线段的长度的倒数和与焦点弦的倾斜程度好象没有关系,那么这样的猜想到底对还是错呢?若这个猜想是正确的,那么这样的倒数和到底是多少呢?下面我以焦点在 轴正半轴的标准抛物线来研究这个问题 轴正半轴的标准抛物线来研究这个问题
题目:过抛物线 的焦点 的焦点 作直线交抛物线于 作直线交抛物线于 两点,且 两点,且 试求 试求 的值. 的值.
探究:因为直线 可以垂直于 可以垂直于 轴,故我们有必要先分类讨论. 轴,故我们有必要先分类讨论.
(一).若直线 垂直于 垂直于 轴.如图1,若 轴.如图1,若 轴,由 轴,由 易得 易得 .则 .则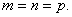 于是,有 于是,有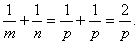

到这里,我们可以猜测,  若为定值的话,那么这个值估计就是 若为定值的话,那么这个值估计就是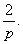 下面对一般情形进行分析. 下面对一般情形进行分析.
(二).如图2,令直线 的倾斜角为 的倾斜角为

方法一 令 在 在 轴上的射影分别为 轴上的射影分别为 在准线上的射影分别为 在准线上的射影分别为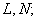 准线与 准线与 轴的交点为 轴的交点为 由抛物线的定义,有 由抛物线的定义,有 ,又四边形 ,又四边形 为矩形,有 为矩形,有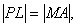 则 则 而 而 .于是 .于是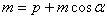 ,解此关于 ,解此关于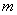 的方程,得 的方程,得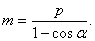 同理: 同理: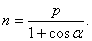 则 则 为定值. 为定值.
当然,在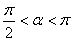 时,同理可以证明这个结论.结论成立,在证明此结论的过程中,还得到了一个副产品,即: 时,同理可以证明这个结论.结论成立,在证明此结论的过程中,还得到了一个副产品,即: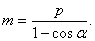 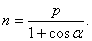 由 由  .当 .当 时, 时,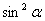 最大,则 最大,则 最小,此时,称 最小,此时,称 为通径. 为通径.
在研究一般情形时,还可以采用下面一种方法,也是比较简便的.

方法二 如图3,不妨仍令直线 的倾斜角为 的倾斜角为  点在 点在 上的射影为 上的射影为 易知 易知 则 则
整理,得 ,即 ,即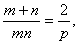 有 有
当然,在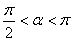 时,同理可以证明这个结论.结论成立. 时,同理可以证明这个结论.结论成立.
(责任编辑:admin) |




