|
湖南省常德市安乡县第五中学 龚光勇收集整理 15．正弦函数  、余弦函数 的性质：（1）定义域：都是R。 （2）值域：都是  ，对 ，当 时， 取最大值1；当 时，取最小值－1；对 ，当 时，取最大值1，当 时，取最小值－1。比如：①若函数  的最大值为 ，最小值为 ，则 __， ＿（答： 或 ）；②函数  （ ）的值域是____（答：[－1, 2]）；③若  ，则 的最大值和最小值分别是____ 、_____（答：7；－5）；④函数   的最小值是_____，此时 ＝__________（答：2； ）；⑤己知  ，求 的变化范围（答： ）；⑥若  ，求 的最大、最小值（答： ， ）。特别提醒：在解含有正余弦函数的问题时，你深入挖掘正余弦函数的有界性了吗？ （3）周期性：① 、的最小正周期都是2 ；② 和 的最小正周期都是 。比如：①若  ，则 ＝___（答：0）；②函数    的最小正周期为____（答：）；③设函数  ，若对任意 都有 成立，则 的最小值为____（答：2）（4）奇偶性与对称性：正弦函数 是奇函数，对称中心是 ，对称轴是直线 ；余弦函数是偶函数，对称中心是 ，对称轴是直线 （正(余)弦型函数的对称轴为过最高点或最低点且垂直于轴的直线，对称中心为图象与轴的交点）。比如：①函数  的奇偶性是______（答：偶函数）；②已知函数  为常数），且 ，则 ______（答：－5）；③函数  的图象的对称中心和对称轴分别是__________、____________（答： 、 ）；④已知  为偶函数，求 的值。（答： ）（5）单调性：  上单调递增，在 单调递减；在 上单调递减，在 上单调递增。特别提醒，别忘了  ！ 16．形如  的函数：（1）几个物理量：A―振幅；  ―频率（周期的倒数）； ―相位； ―初相；（2）函数 表达式的确定：A由最值确定； 由周期确定；由图象上的特殊点确定，如 ， 的图象如图所示，则 ＝_____（答： ）； （3）函数 图象的画法：①“五点法”――设 ，令 ＝0， 求出相应的值，计算得出五点的坐标，描点后得出图象；②图象变换法：这是作函数简图常用方法。（4）函数  的图象与图象间的关系：①函数的图象纵坐标不变，横坐标向左（>0）或向右（<0）平移 个单位得 的图象；②函数图象的纵坐标不变，横坐标变为原来的 ，得到函数 的图象；③函数图象的横坐标不变，纵坐标变为原来的A倍，得到函数的图象；④函数图象的横坐标不变，纵坐标向上（ ）或向下（ ），得到 的图象。要特别注意，若由 得到的图象，则向左或向右平移应平移 个单位。比如：①函数  的图象经过怎样的变换才能得到的图象？（答：向上平移1个单位得 的图象，再向左平移 个单位得 的图象，横坐标扩大到原来的2倍得 的图象，最后将纵坐标缩小到原来的 即得的图象）；②要得到函数  的图象，只需把函数 的图象向___平移____个单位（答：左； ）；③将函数  图像，按向量 平移后得到的函数图像关于原点对称，这样的向量是否唯一？若唯一，求出；若不唯一，求出模最小的向量（答：存在但不唯一，模最小的向量 ）；④若函数  的图象与直线 有且仅有四个不同的交点，则 的取值范围是 （答： ）（5）研究函数 性质的方法：类比于研究的性质，只需将中的看成中的，但在求的单调区间时，要特别注意A和的符号，通过诱导公式先将化正。比如：①函数  的递减区间是______（答： ）；②  的递减区间是_______（答： ）；③设函数  的图象关于直线 对称，它的周期是，则A、  B、在区间 上是减函数 C、  D、的最大值是A（答：C）④对于函数  给出下列结论：①图象关于原点成中心对称；②图象关于直线 成轴对称；③图象可由函数的图像向左平移 个单位得到；④图像向左平移 个单位，即得到函数 的图像。其中正确结论是_______（答：②④）；⑤已知函数  图象与直线 的交点中，距离最近两点间的距离为，那么此函数的周期是_______（答：）17．正切函数  的图象和性质：（1）定义域：  。遇到有关正切函数问题时，你注意到正切函数的定义域了吗？（2）值域是R，在上面定义域上无最大值也无最小值； （3）周期性：是周期函数且周期是 ，它与直线 的两个相邻交点之间的距离是一个周期。绝对值或平方对三角函数周期性的影响：一般说来，某一周期函数解析式加绝对值或平方，其周期性是：弦减半、切不变．既为周期函数又是偶函数的函数自变量加绝对值，其周期性不变，其它不定。如  的周期都是, 但  的周期为，而 ， 的周期不变；（4）奇偶性与对称性：是奇函数，对称中心是   ，特别提醒：正(余)切型函数的对称中心有两类：一类是图象与轴的交点，另一类是渐近线与轴的交点，但无对称轴，这是与正弦、余弦函数的不同之处。（5）单调性：正切函数在开区间 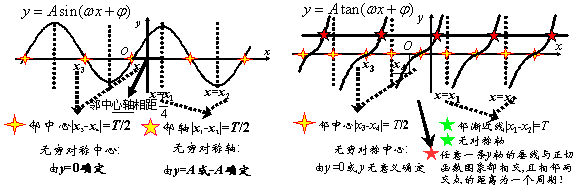 内都是增函数。但要注意在整个定义域上不具有单调性。如下图：  18．三角形中的有关公式： (1)内角和定理：三角形三角和为 ，这是三角形中三角函数问题的特殊性，解题可不能忘记！任意两角和与第三个角总互补，任意两半角和与第三个角的半角总互余.锐角三角形 三内角都是锐角三内角的余弦值为正值任两角和都是钝角任意两边的平方和大于第三边的平方。(2)正弦定理：  (R为三角形外接圆的半径).注意：①正弦定理的一些变式： ；  ； ；②已知三角形两边一对角，求解三角形时，若运用正弦定理，则务必注意可能有两解。(3)余弦定理：  等，常选用余弦定理鉴定三角形的形状。(4)面积公式：  （其中 为三角形内切圆半径）.如 中，若 ，判断的形状（答：直角三角形）。特别提醒：（1）求解三角形中的问题时，一定要注意  这个特殊性： ；（2）求解三角形中含有边角混合关系的问题时，常运用正弦定理、余弦定理实现边角互化。比如：①  中，A、B的对边分别是 ，且 ，那么满足条件的 A、 有一个解 B、有两个解 C、无解 D、不能确定（答：C）； ②在 中，A＞B是 成立的_____条件（答：充要）；③在 中，  ，则 ＝_____（答： ）；④在 中， 分别是角A、B、C所对的边，若  ，则 ＝____（答： ）；⑤在 中，若其面积 ，则=____（答： ）；⑥在 中， ，这个三角形的面积为 ，则外接圆的直径是_______（答： ）；⑦在△ABC中，a、b、c是角A、B、C的对边，  = ， 的最大值为 （答： ）；⑧在△ABC中AB=1，BC=2，则角C的取值范围是 （答：  ）；⑨设O是锐角三角形ABC的外心，若  ，且 的面积满足关系式 ，求 （答： ）。19．反三角函数：（1）反三角函数的定义（以反正弦函数为例）：  表示一个角，这个角的正弦值为 ,且这个角在 内 。(2)反正弦 、反余弦 、反正切 的取值范围分别是 。在用反三角表示两异面直线所成的角、直线与平面所成的角、二面角的平面角、直线的倾斜角、  到 的角、与的夹角以及两向量的夹角时，你是否注意到了它们的范围？ ， ，  。20．求角的方法：先确定角的范围，再求出关于此角的某一个三角函数（要注意选择，其标准有二：一是此三角函数在角的范围内具有单调性；二是根据条件易求出此三角函数值）。比如： （1）若  ，且 、 是方程 的两根，则求 的值______（答： ）；（2） 中， ，则＝_______（答：）；（3）若  且 ， ，求 的值（答： ）.(责任编辑：admin) |