湖南省常德市安乡县第五中学 龚光勇收集整理
1.角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。射线的起始位置称为始边,终止位置称为终边。
2.象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与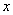 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。
3.终边相同的角的表示:
(1) 终边与 终边与 终边相同( 终边相同( 的终边在 的终边在 终边所在射线上) 终边所在射线上)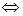  ,注意:相等的角的终边一定相同,终边相同的角不一定相等。 ,注意:相等的角的终边一定相同,终边相同的角不一定相等。
如与角 的终边相同,且绝对值最小的角的度数是___,合___弧度。(答: 的终边相同,且绝对值最小的角的度数是___,合___弧度。(答: ; ; ) )
(2) 终边与 终边与 终边共线( 终边共线( 的终边在 的终边在 终边所在直线上) 终边所在直线上) 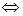 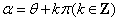 。 。
(3) 终边与 终边与 终边关于 终边关于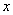 轴对称 轴对称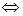 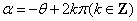 。 。
(4) 终边与 终边与 终边关于 终边关于 轴对称 轴对称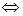 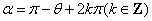 。 。
(5) 终边与 终边与 终边关于原点对称 终边关于原点对称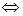  。 。
(6) 终边在 终边在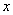 轴上的角可表示为: 轴上的角可表示为: ; ; 终边在 终边在 轴上的角可表示为: 轴上的角可表示为: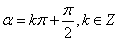 ; ; 终边在坐标轴上的角可表示为: 终边在坐标轴上的角可表示为: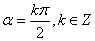 。 。
如 的终边与 的终边与 的终边关于直线 的终边关于直线 对称,则 对称,则 =____________。(答: =____________。(答: ) )
4. 与 与 的终边关系:由“两等分各象限、一二三四”确定。 的终边关系:由“两等分各象限、一二三四”确定。
如若 是第二象限角,则 是第二象限角,则 是第_____象限角(答:一、三) 是第_____象限角(答:一、三)
5.弧长公式: ,扇形面积公式: ,扇形面积公式: ,1弧度(1rad) ,1弧度(1rad) 。 。
如已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。(答:2 ) )
6.任意角的三角函数的定义:设 是任意一个角,P 是任意一个角,P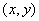 是 是 的终边上的任意一点(异于原点),它与原点的距离是 的终边上的任意一点(异于原点),它与原点的距离是 ,那么 ,那么
 , ,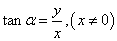 , ,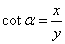  , ,
  , ,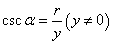 。 。
三角函数值只与角的大小有关,而与终边上点P的位置无关。
如(1)已知角 的终边经过点P(5,-12),则 的终边经过点P(5,-12),则 的值为__。(答: 的值为__。(答: );(2)设 );(2)设 是第三、四象限角, 是第三、四象限角, ,则 ,则 的取值范围是_______(答:(-1, 的取值范围是_______(答:(-1,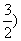 );(3)若 );(3)若 ,试判断 ,试判断 的符号(答:负) 的符号(答:负)
7.三角函数线的特征是:正弦线MP“站在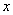 轴上(起点在 轴上(起点在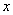 轴上)”、余弦线OM“躺在 轴上)”、余弦线OM“躺在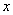 轴上(起点是原点)”、正切线AT“站在点 轴上(起点是原点)”、正切线AT“站在点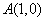 处(起点是 处(起点是 )”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。 )”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。

如(1)若 ,则 ,则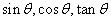 的大小关系为_____(答: 的大小关系为_____(答: );(2)若 );(2)若 为锐角,则 为锐角,则 的大小关系为_______ (答: 的大小关系为_______ (答: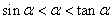 );(3)函数 );(3)函数 的定义域是_______(答: 的定义域是_______(答: ) )
8.特殊角的三角函数值:
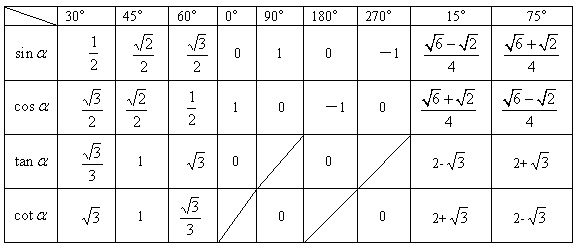
9 同角三角函数的基本关系式:
(1)平方关系:
(2)倒数关系:sin csc csc =1,cos =1,cos sec sec =1,tan =1,tan cot cot =1, =1,
(3)商数关系:
同角三角函数的基本关系式的主要应用是,已知一个角的三角函数值,求此角的其它三角函数值。在运用平方关系解题时,要根据已知角的范围和三角函数的取值,尽可能地压缩角的范围,以便进行定号;在具体求三角函数值时,一般不需用同角三角函数的基本关系式,而是先根据角的范围确定三角函数值的符号,再利用解直角三角形求出此三角函数值的绝对值。比如:
(1)函数 的值的符号为____(答:大于0); 的值的符号为____(答:大于0);
(2)若 ,则使 ,则使 成立的 成立的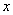 的取值范围是____(答: 的取值范围是____(答: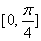   ); );
(3)已知 , , ,则 ,则 =____(答: =____(答: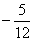 ); );
(4)已知 ,则 ,则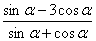 =____; =____;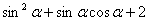 =_________(答: =_________(答: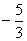 ; ; ); );
(5)已知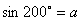 ,则 ,则 等于 等于
A、 B、 B、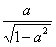 C、 C、 D、 D、 (答:B); (答:B);
(6)已知 ,则 ,则 的值为______(答:-1)。 的值为______(答:-1)。
10.三角函数诱导公式( )的本质是:奇变偶不变(对 )的本质是:奇变偶不变(对 而言,指 而言,指 取奇数或偶数),符号看象限(看原函数,同时可把 取奇数或偶数),符号看象限(看原函数,同时可把 看成是锐角).诱导公式的应用是求任意角的三角函数值,其一般步骤:(1)负角变正角,再写成2k 看成是锐角).诱导公式的应用是求任意角的三角函数值,其一般步骤:(1)负角变正角,再写成2k + + , ,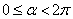 ;(2)转化为锐角三角函数。比如: ;(2)转化为锐角三角函数。比如:
(1) 的值为________(答: 的值为________(答: ); );
(2)已知 ,则 ,则 ______,若 ______,若 为第二象限角, 为第二象限角,
则 ________。(答: ________。(答: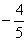 ; ; ) )
11.两角和与差的正弦、余弦、正切公式及倍角公式:


比如:
(1)下列各式中,值为 的是 的是
A、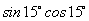 B、 B、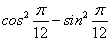 C、 C、 D、 D、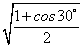 (答:C); (答:C);
(2)命题P: ,命题Q: ,命题Q: ,则P是Q的 ,则P是Q的
A、充要条件 B、充分不必要条件 C、必要不充分条件 D、既不充分也不必要条件(答:C);
(3)已知 ,那么 ,那么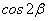 的值为____(答: 的值为____(答: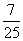 ); );
(4)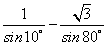 的值是______(答:4); 的值是______(答:4);
(5)已知 ,求 ,求 的值(用a表示)甲求得的结果是 的值(用a表示)甲求得的结果是 ,乙求得的结果是 ,乙求得的结果是 ,对甲、乙求得的结果的正确性你的判断是______(答:甲、乙都对) ,对甲、乙求得的结果的正确性你的判断是______(答:甲、乙都对)
12. 三角函数的化简、计算、证明的恒等变形的基本思路是:一角二名三结构。即首先观察角与角之间的关系,注意角的一些常用变式,角的变换是三角函数变换的核心!第二看函数名称之间的关系,通常“切化弦”;第三观察代数式的结构特点。基本的技巧有:
(1)巧变角(已知角与特殊角的变换、已知角与目标角的变换、角与其倍角的变换、两角与其和差角的变换.。
如 , ,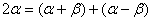 , , , ,
 , , 等),比如: 等),比如:
①已知 , ,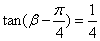 ,那么 ,那么 的值是_____(答: 的值是_____(答: ); );
②已知 ,且 ,且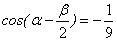 , , ,求 ,求 的值(答: 的值(答: ); );
③已知 为锐角, 为锐角, , , ,则 ,则 与 与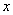 的函数关系为______(答: 的函数关系为______(答: ) )
(2)三角函数名互化(切割化弦),比如:
①求值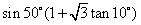 (答:1); (答:1);
②已知 ,求 ,求 的值(答: 的值(答: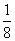 ) )
(3)公式变形使用( 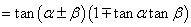 。比如: 。比如:
①已知A、B为锐角,且满足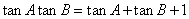 ,则 ,则 =_____(答: =_____(答: ); );
②设 中, 中, , , ,则此三角形是____三角形(答:等边) ,则此三角形是____三角形(答:等边)
(4)三角函数次数的降升(降幂公式: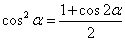 , , 与升幂公式: 与升幂公式: , , )。比如: )。比如:
①若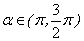 ,化简 ,化简 为_____(答: 为_____(答: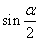 ); );
②函数  的单调递增区间为___________(答: 的单调递增区间为___________(答: ) )
(5)式子结构的转化(对角、函数名、式子结构化同)。比如:
①  (答: (答: ); );
②求证: ; ;
③化简: (答: (答: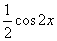 ) )
(6)常值变换主要指“1”的变换(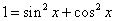 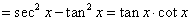
 等)。 等)。
如已知 ,求 ,求 (答: (答: )。 )。
(7)正余弦“三兄妹— ”的内存联系――“知一求二”,比如: ”的内存联系――“知一求二”,比如:
①若  ,则 ,则 __(答: __(答: ); );
特别提醒:这里 ; ;
②若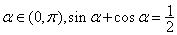 ,求 ,求 的值。(答: 的值。(答: ); );
③已知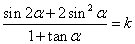 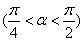 ,试用 ,试用 表示 表示 的值(答: 的值(答: )。 )。
13.辅助角公式中辅助角的确定: (其中 (其中 角所在的象限由a, b的符号确定, 角所在的象限由a, b的符号确定, 角的值由 角的值由 确定)在求最值、化简时起着重要作用。比如: 确定)在求最值、化简时起着重要作用。比如:
(1)若方程 有实数解,则 有实数解,则 的取值范围是___________.(答:[-2,2]); 的取值范围是___________.(答:[-2,2]);
(2)当函数 取得最大值时, 取得最大值时, 的值是______(答: 的值是______(答: ); );
(3)如果 是奇函数,则 是奇函数,则 = (答:-2); = (答:-2);
(4)求值: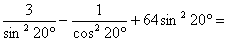 ________(答:32) ________(答:32)
14.正弦函数和余弦函数的图象:正弦函数 和余弦函数 和余弦函数 图象的作图方法:五点法:先取横坐标分别为0, 图象的作图方法:五点法:先取横坐标分别为0, 的五点,再用光滑的曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象。 的五点,再用光滑的曲线把这五点连接起来,就得到正弦曲线和余弦曲线在一个周期内的图象。
(责任编辑:admin) |



 为_____(答:
为_____(答: ;
; (答:
(答: