|
贵州省黄平县旧州中学 杨胜万 在人教大纲版高二数学上册中,关于点到直线距离公式的推导方法,教材介绍了两种推导方法,并详细给出了利用直角三角形的面积公式推导得出点到直线的距离公式的具体过程。其实关于点到直线的距离公式的推导方法，除上述方法之外，还有其它很多方法，在这些方法中，向量法（利用平面向量的有关知识来推导的方法）是一种行之有效的推导方法。其推导思路简单明了、运算量也较小。下面笔者给出向量法推导点到直线的距离的具体过程，以供同行参考： 已知直线 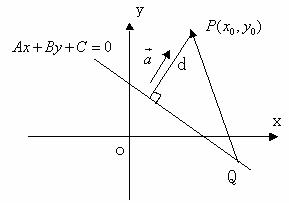 ： 和点 ， 为点 到直线的距离。现不妨设 且 ，则直线的斜率为 ，其方向向量为 ，从而易知其法向量 ，又设点 为直线上的任一点（如图所示），于是有：  由平面向量的有关知识，可得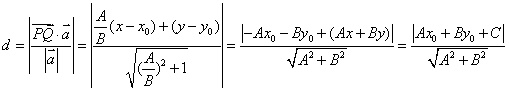：  显然，当 或时，上述公式仍成立。上述推导方法利用了向量的数量积知识来进行推导出了点到直线的距离公式，这是一种比较重要有数学思想方法。我们还可将这种思想方法进一步推广到在立体几何中，如何利用空间向量解决求点到平面的距离问题。 (责任编辑：admin) |