湖南省常德市安乡县第五中学 龚光勇收集整理
1.直线的倾斜角:(1)定义:在平面直角坐标系中,对于一条与 轴相交的直线 轴相交的直线 ,如果把 ,如果把 轴绕着交点按逆时针方向转到和直线 轴绕着交点按逆时针方向转到和直线 重合时所转的最小正角记为 重合时所转的最小正角记为 ,那么 ,那么 就叫做直线的倾斜角。当直线 就叫做直线的倾斜角。当直线 与 与 轴重合或平行时,规定倾斜角为0;(2)倾斜角的范围 轴重合或平行时,规定倾斜角为0;(2)倾斜角的范围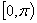 。比如: 。比如:
(1)直线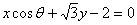 的倾斜角的范围是____(答: 的倾斜角的范围是____(答: ); );
(2)过点 的直线的倾斜角的范围 的直线的倾斜角的范围 值的范围是______(答: 值的范围是______(答: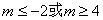 ) )
2.直线的斜率:
(1)定义:倾斜角不是90°的直线,它的倾斜角的正切值叫这条直线的斜率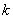 ,即 ,即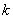 =tan =tan ( ( ≠90°);倾斜角为90°的直线没有斜率; ≠90°);倾斜角为90°的直线没有斜率;
(2)斜率公式:经过两点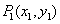 、 、 的直线的斜率为 的直线的斜率为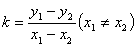 ; ;
(3)直线的方向向量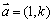 ,直线的方向向量与直线的斜率有何关系? ,直线的方向向量与直线的斜率有何关系?
(4)应用:证明三点共线: 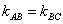 。 。
如(1) 两条直线钭率相等是这两条直线平行的____________条件(答:既不充分也不必要);(2)实数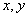 满足 满足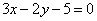 ( ( ),则 ),则 的最大值、最小值分别为______(答: 的最大值、最小值分别为______(答: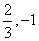 ) )
3.直线的方程:
(1)点斜式:已知直线过点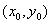 斜率为 斜率为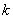 ,则直线方程为 ,则直线方程为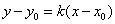 ,它不包括垂直于 ,它不包括垂直于 轴的直线。 轴的直线。
(2)斜截式:已知直线在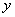 轴上的截距为 轴上的截距为 和斜率 和斜率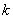 ,则直线方程为 ,则直线方程为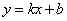 ,它不包括垂直于 ,它不包括垂直于 轴的直线。 轴的直线。
(3)两点式:已知直线经过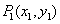 、 、 两点,则直线方程为 两点,则直线方程为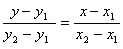 ,它不包括垂直于坐标轴的直线。 ,它不包括垂直于坐标轴的直线。
(4)截距式:已知直线在 轴和 轴和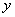 轴上的截距为 轴上的截距为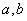 ,则直线方程为 ,则直线方程为 ,它不包括垂直于坐标轴的直线和过原点的直线。 ,它不包括垂直于坐标轴的直线和过原点的直线。
(5)一般式:任何直线均可写成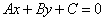 (A,B不同时为0)的形式。 (A,B不同时为0)的形式。
如(1)经过点(2,1)且方向向量为 =(-1, =(-1,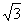 )的直线的点斜式方程是___________(答: )的直线的点斜式方程是___________(答: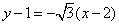 );(2)直线 );(2)直线 ,不管 ,不管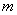 怎样变化恒过点______(答: 怎样变化恒过点______(答: );(3)若曲线 );(3)若曲线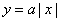 与 与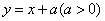 有两个公共点,则 有两个公共点,则 的取值范围是_______(答: 的取值范围是_______(答: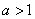 ) )
提醒:(1)直线方程的各种形式都有局限性.(如点斜式不适用于斜率不存在的直线,还有截距式呢?);(2)直线在坐标轴上的截距可正、可负、也可为0.直线两截距相等 直线的斜率为-1或直线过原点;直线两截距互为相反数 直线的斜率为-1或直线过原点;直线两截距互为相反数 直线的斜率为1或直线过原点;直线两截距绝对值相等 直线的斜率为1或直线过原点;直线两截距绝对值相等 直线的斜率为 直线的斜率为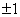 或直线过原点。 或直线过原点。
如过点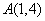 ,且纵横截距的绝对值相等的直线共有___条(答:3) ,且纵横截距的绝对值相等的直线共有___条(答:3)
4.设直线方程的一些常用技巧:
(1)知直线纵截距 ,常设其方程为 ,常设其方程为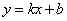 ; ;
(2)知直线横截距 ,常设其方程为 ,常设其方程为 (它不适用于斜率为0的直线); (它不适用于斜率为0的直线);
(3)知直线过点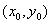 ,当斜率 ,当斜率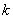 存在时,常设其方程为 存在时,常设其方程为 ,当斜率 ,当斜率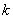 不存在时,则其方程为 不存在时,则其方程为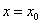 ; ;
(4)与直线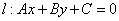 平行的直线可表示为 平行的直线可表示为 ; ;
(5)与直线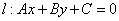 垂直的直线可表示为 垂直的直线可表示为 . .
提醒:求直线方程的基本思想和方法是恰当选择方程的形式,利用待定系数法求解。
5.点到直线的距离及两平行直线间的距离:
(1)点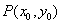 到直线 到直线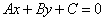 的距离 的距离 ; ;
(2)两平行线 间的距离为 间的距离为 。 。
6.直线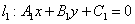 与直线 与直线 的位置关系: 的位置关系:
(1)平行 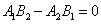 (斜率)且 (斜率)且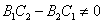 (在 (在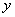 轴上截距); 轴上截距);
(2)相交 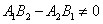 ; ;
(3)重合 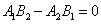 且 且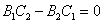 。 。
提醒:(1) 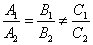 、 、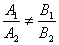 、 、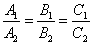 仅是两直线平行、相交、重合的充分不必要条件!为什么?(2)在解析几何中,研究两条直线的位置关系时,有可能这两条直线重合,而在立体几何中提到的两条直线都是指不重合的两条直线;(3)直线 仅是两直线平行、相交、重合的充分不必要条件!为什么?(2)在解析几何中,研究两条直线的位置关系时,有可能这两条直线重合,而在立体几何中提到的两条直线都是指不重合的两条直线;(3)直线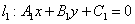 与直线 与直线 垂直 垂直  。 。
如(1)设直线 和 和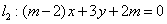 ,当 ,当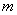 =_______时 =_______时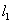 ∥ ∥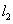 ;当 ;当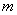 =________时 =________时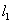 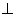 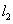 ;当 ;当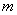 _________时 _________时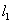 与 与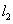 相交;当 相交;当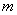 =_________时 =_________时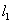 与 与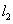 重合(答:-1; 重合(答:-1;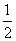 ; ;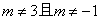 ;3);(2)已知直线 ;3);(2)已知直线 的方程为 的方程为 ,则与 ,则与 平行,且过点(—1,3)的直线方程是______(答: 平行,且过点(—1,3)的直线方程是______(答: );(3)两条直线 );(3)两条直线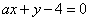 与 与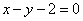 相交于第一象限,则实数 相交于第一象限,则实数 的取值范围是____(答: 的取值范围是____(答: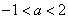 );(4)设 );(4)设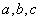 分别是△ABC中∠A、∠B、∠C所对边的边长,则直线 分别是△ABC中∠A、∠B、∠C所对边的边长,则直线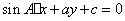 与 与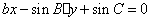 的位置关系是____(答:垂直);(5)已知点 的位置关系是____(答:垂直);(5)已知点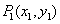 是直线 是直线 上一点, 上一点, 是直线 是直线 外一点,则方程 外一点,则方程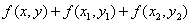 =0所表示的直线与 =0所表示的直线与 的关系是____(答:平行);(6)直线 的关系是____(答:平行);(6)直线 过点(1,0),且被两平行直线 过点(1,0),且被两平行直线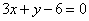 和 和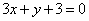 所截得的线段长为9,则直线 所截得的线段长为9,则直线 的方程是________(答: 的方程是________(答: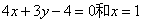 ) )
7.到角和夹角公式:(1)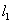 到 到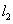 的角是指直线 的角是指直线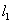 绕着交点按逆时针方向转到和直线 绕着交点按逆时针方向转到和直线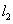 重合所转的角 重合所转的角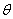 , ,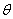  且tan 且tan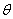 = =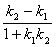 ( (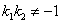 );(2) );(2)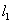 与 与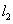 的夹角是指不大于直角的角 的夹角是指不大于直角的角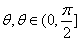 且tan 且tan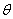 =︱ =︱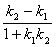 ︱( ︱(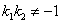 )。 )。
提醒:解析几何中角的问题常用到角公式或向量知识求解。
如已知点M是直线 与 与 轴的交点,把直线 轴的交点,把直线 绕点M逆时针方向旋转45°,得到的直线方程是______(答: 绕点M逆时针方向旋转45°,得到的直线方程是______(答: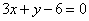 ) )
8.对称(中心对称和轴对称)问题——代入法:比如:
(1)已知点 与点 与点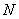 关于 关于 轴对称,点P与点N关于 轴对称,点P与点N关于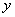 轴对称,点Q与点P关于直线 轴对称,点Q与点P关于直线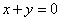 对称,则点Q的坐标为_______(答: 对称,则点Q的坐标为_______(答: ); );
(2)已知直线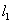 与 与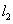 的夹角平分线为 的夹角平分线为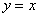 ,若 ,若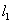 的方程为 的方程为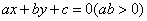 ,那么 ,那么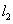 的方程是___________(答: 的方程是___________(答: ); );
(3)点A(4,5)关于直线 的对称点为B(-2,7),则 的对称点为B(-2,7),则 的方程是_________(答: 的方程是_________(答: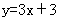 ); );
(4)已知一束光线通过点A(-3,5),经直线 :3x-4y+4=0反射。如果反射光线通过点B(2,15),则反射光线所在直线的方程是_________(答: :3x-4y+4=0反射。如果反射光线通过点B(2,15),则反射光线所在直线的方程是_________(答: ); );
(5)已知ΔABC顶点A(3,-1),AB边上的中线所在直线的方程为6x+10y-59=0,∠B的平分线所在的方程为x-4y+10=0,求BC边所在的直线方程(答: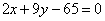 ); );
(6)直线2x―y―4=0上有一点P,它与两定点A(4,-1)、B(3,4)的距离之差最大,则P的坐标是______(答:(5,6));
(7)已知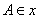 轴, 轴, ,C(2,1), ,C(2,1),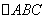 周长的最小值为______(答: 周长的最小值为______(答: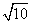 )。 )。
提醒:在解几中遇到角平分线、光线反射等条件常利用对称求解。
9.简单的线性规划:
(1)二元一次不等式表示的平面区域:①法一:先把二元一次不等式改写成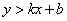 或 或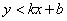 的形式,前者表示直线的上方区域,后者表示直线的下方区域;法二:用特殊点判断;②无等号时用虚线表示不包含直线 的形式,前者表示直线的上方区域,后者表示直线的下方区域;法二:用特殊点判断;②无等号时用虚线表示不包含直线 ,有等号时用实线表示包含直线 ,有等号时用实线表示包含直线 ;③设点 ;③设点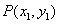 , ,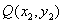 ,若 ,若 与 与 同号,则P,Q在直线 同号,则P,Q在直线 的同侧,异号则在直线 的同侧,异号则在直线 的异侧。 的异侧。
如已知点A(—2,4),B(4,2),且直线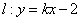 与线段AB恒相交,则 与线段AB恒相交,则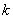 的取值范围是__________(答: 的取值范围是__________(答: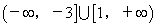 ) )
(2)线性规划问题中的有关概念:
①满足关于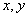 的一次不等式或一次方程的条件叫线性约束条件。 的一次不等式或一次方程的条件叫线性约束条件。
②关于变量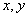 的解析式叫目标函数,关于变量 的解析式叫目标函数,关于变量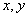 一次式的目标函数叫线性目标函数; 一次式的目标函数叫线性目标函数;
③求目标函数在线性约束条件下的最大值或最小值的问题,称为线性规划问题;
④满足线性约束条件的解(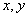 )叫可行解,由所有可行解组成的集合叫做可行域; )叫可行解,由所有可行解组成的集合叫做可行域;
⑤使目标函数取得最大值或最小值的可行解叫做最优解;
(3)求解线性规划问题的步骤是什么?①根据实际问题的约束条件列出不等式;②作出可行域,写出目标函数;③确定目标函数的最优位置,从而获得最优解。比如:
①线性目标函数z=2x-y在线性约束条件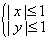 下,取最小值的最优解是____(答:(-1,1)); 下,取最小值的最优解是____(答:(-1,1));
②点(-2,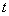 )在直线2x-3y+6=0的上方,则 )在直线2x-3y+6=0的上方,则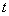 的取值范围是_________(答: 的取值范围是_________(答: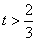 ); );
③不等式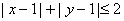 表示的平面区域的面积是_________(答:8); 表示的平面区域的面积是_________(答:8);
④如果实数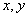 满足 满足 ,则 ,则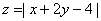 的最大值_________(答:21) 的最大值_________(答:21)
(4)在求解线性规划问题时要注意:①将目标函数改成斜截式方程;②寻找最优解时注意作图规范。
10.圆的方程:
⑴圆的标准方程: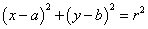 。 。
⑵圆的一般方程: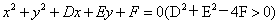 ,特别提醒:只有当 ,特别提醒:只有当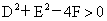 时,方程 时,方程 才表示圆心为 才表示圆心为 ,半径为 ,半径为 的圆(二元二次方程 的圆(二元二次方程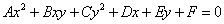 表示圆的充要条件是什么? ( 表示圆的充要条件是什么? (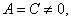 且 且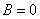 且 且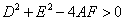 )); ));
⑶圆的参数方程: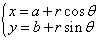 ( (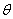 为参数),其中圆心为 为参数),其中圆心为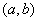 ,半径为 ,半径为 。圆的参数方程的主要应用是三角换元: 。圆的参数方程的主要应用是三角换元: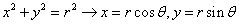 ; ;
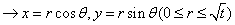 。 。
⑷ 为直径端点的圆方程 为直径端点的圆方程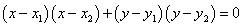
比如:
(1)圆C与圆 关于直线 关于直线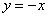 对称,则圆C的方程为____________(答: 对称,则圆C的方程为____________(答: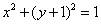 ); );
(2)圆心在直线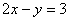 上,且与两坐标轴均相切的圆的标准方程是__________(答: 上,且与两坐标轴均相切的圆的标准方程是__________(答: 或 或 ); );
(3)已知 是圆 是圆 ( (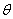 为参数, 为参数, 上的点,则圆的普通方程为________,P点对应的 上的点,则圆的普通方程为________,P点对应的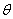 值为_______,过P点的圆的切线方程是___________(答: 值为_______,过P点的圆的切线方程是___________(答: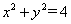 ; ;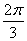 ; ;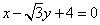 ); );
(4)如果直线 将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么 将圆:x2+y2-2x-4y=0平分,且不过第四象限,那么 的斜率的取值范围是____(答:[0,2]); 的斜率的取值范围是____(答:[0,2]);
(5)方程x2+y2-x+y+k=0表示一个圆,则实数k的取值范围为____(答: ); );
(6)若 ( (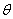 为参数, 为参数,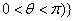 , ,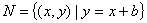 ,若 ,若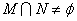 ,则b的取值范围是_________(答: ,则b的取值范围是_________(答: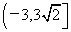 ) )
11.点与圆的位置关系:已知点 及圆 及圆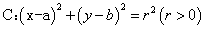 ,(1)点M在圆C外 ,(1)点M在圆C外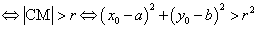 ;(2)点M在圆C内 ;(2)点M在圆C内
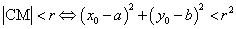 ;(3)点M在圆C上 ;(3)点M在圆C上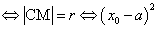
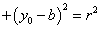 。 。
如点P(5a+1,12a)在圆(x-1)2+y2=1的内部,则a的取值范围是______(答: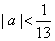 ) )
12.直线与圆的位置关系:直线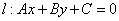 和圆 和圆  有相交、相离、相切。可从代数和几何两个方面来判断:(1)代数方法(判断直线与圆方程联立所得方程组的解的情况): 有相交、相离、相切。可从代数和几何两个方面来判断:(1)代数方法(判断直线与圆方程联立所得方程组的解的情况):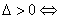 相交; 相交;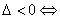 相离; 相离;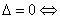 相切;(2)几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为 相切;(2)几何方法(比较圆心到直线的距离与半径的大小):设圆心到直线的距离为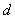 ,则 ,则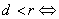 相交; 相交; 相离; 相离; 相切。 相切。
提醒:判断直线与圆的位置关系一般用几何方法较简捷。比如:
(1)圆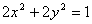 与直线 与直线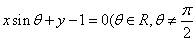  , ,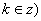 的位置关系为____(答:相离); 的位置关系为____(答:相离);
(2)若直线 与圆 与圆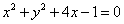 切于点 切于点 ,则 ,则 的值____(答:2); 的值____(答:2);
(3)直线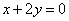 被曲线 被曲线  所截得的弦长等于 (答: 所截得的弦长等于 (答: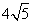 ); );
(4)一束光线从点A(-1,1)出发经x轴反射到圆C:(x-2)2+(y-3)2=1上的最短路程是 (答:4);
(5)已知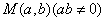 是圆 是圆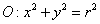 内一点,现有以 内一点,现有以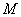 为中点的弦所在直线 为中点的弦所在直线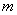 和直线 和直线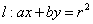 ,则 ,则
A.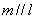 ,且 ,且 与圆相交 B. 与圆相交 B. ,且 ,且 与圆相交 与圆相交
C.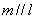 ,且 ,且 与圆相离 D. 与圆相离 D. ,且 ,且 与圆相离(答:C); 与圆相离(答:C);
(6)已知圆C: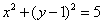 ,直线L: ,直线L: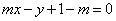 。①求证:对 。①求证:对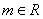 ,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若 ,直线L与圆C总有两个不同的交点;②设L与圆C交于A、B两点,若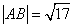 ,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程. (答:② ,求L的倾斜角;③求直线L中,截圆所得的弦最长及最短时的直线方程. (答:②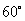 或 或 ③最长: ③最长: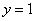 ,最短: ,最短: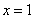 ) )
13.圆与圆的位置关系(用两圆的圆心距与半径之间的关系判断):已知两圆的圆心分别为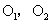 ,半径分别为 ,半径分别为 ,则(1)当 ,则(1)当 时,两圆外离;(2)当 时,两圆外离;(2)当 时,两圆外切;(3)当 时,两圆外切;(3)当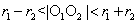 时,两圆相交;(4)当 时,两圆相交;(4)当 时,两圆内切;(5)当 时,两圆内切;(5)当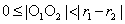 时,两圆内含。 时,两圆内含。
如双曲线 的左焦点为F1,顶点为A1、A2,P是双曲线右支上任意一点,则分别以线段PF1、A1A2为直径的两圆位置关系为 (答:内切) 的左焦点为F1,顶点为A1、A2,P是双曲线右支上任意一点,则分别以线段PF1、A1A2为直径的两圆位置关系为 (答:内切)
14.圆的切线与弦长:
(1) 切线:
①过圆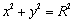 上一点 上一点 圆的切线方程是: 圆的切线方程是: ,过圆 ,过圆 上一点 上一点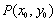 圆的切线方程是: 圆的切线方程是: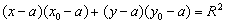 ,一般地,如何求圆的切线方程?(抓住圆心到直线的距离等于半径); ,一般地,如何求圆的切线方程?(抓住圆心到直线的距离等于半径);
②从圆外一点引圆的切线一定有两条,可先设切线方程,再根据相切的条件,运用几何方法(抓住圆心到直线的距离等于半径)来求;③过两切点的直线(即“切点弦”)方程的求法:先求出以已知圆的圆心和这点为直径端点的圆,该圆与已知圆的公共弦就是过两切点的直线方程;
③切线长:过圆 ( ( )外一点 )外一点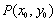 所引圆的切线的长为 所引圆的切线的长为 ( (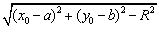 ); );
如设A为圆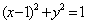 上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为__________(答: 上动点,PA是圆的切线,且|PA|=1,则P点的轨迹方程为__________(答: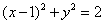 ); );
(2)弦长问题:①圆的弦长的计算:常用弦心距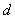 ,弦长一半 ,弦长一半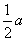 及圆的半径 及圆的半径 所构成的直角三角形来解: 所构成的直角三角形来解: ;②过两圆 ;②过两圆 、 、 交点的圆(公共弦)系为 交点的圆(公共弦)系为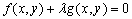 ,当 ,当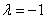 时,方程 时,方程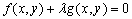 为两圆公共弦所在直线方程.。 为两圆公共弦所在直线方程.。
15.解决直线与圆的关系问题时,要充分发挥圆的平面几何性质的作用(如半径、半弦长、弦心距构成直角三角形,切线长定理、割线定理、弦切角定理等等)。
(责任编辑:admin) |
 ,则
,则