|
学习《万有引力与航天》的常见误区 江西省大余中学 刘庭华 学生在学习《万有引力与航天》内容时，由于对定律的适用条件理解不深刻，或对问题分析不全面，或受思维定势的影响等，解题时常常出现多种错误。下面对学生学习时的常见误区加以归纳，帮助学生扫除障碍。 误区1：忽视万有引力定律的适应条件 例1．假如把一个物体放在地球的球心，则物体受到地球对它的万有引力是多少？ 错解：根据公式  ，把一个物体放在地球的球心处，因为距离r趋向于零，故引力趋向于无穷大。错因分析：万有引力公式适应条件是质点间的引力计算，把物体放在球心，这时不能把地球当成质点，也不能把地球的质量看成集中在球心处理，万有引力定律公式不能直接使用． 正解：可以把地球分成无限份（可视为质点），各部分对物体的引力适用公式条件，由于每一部分受到的引力与关于球心对称的质量相等的那部分对物体的引力平衡，由对称性可得地球对物体的万有引力为零。 误区2：混淆“天体距离”与“轨道半径” 例2．某卫星沿椭圆轨道绕行星运行，近地点离行星中心的距离是a，远地点离行星中心的距离为b，若卫星在近地点的速率为va，则卫星在远地点时的速率vb多少？ 错解：根据卫星运行的向心力由万有引力提供，在近地点时r=a，有  ；在远地点时r=b，有 ，上述两式相比得 ，故 。错因分析：如果卫星绕行星做匀速圆周运动，两者间的距离就是圆周运动的轨道半径。但本题卫星在做椭圆运动，许多同学把卫星在近地点和远地点与行星的距离误认为是卫星运动的轨道半径。 正解：由椭圆的对称性可知，卫星在近地点和远地点的轨道曲率半径是相同的，设曲率半径等于R，则在近地点时有  ，在远地点时有 ，解得 。误区3：对研究对象受力分析不全面 例3．宇宙中存在着一些离其它恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其它星体对它们的引力作用。已观测到稳定的三星系统存在两种基本的构成形式，其中一种是三颗星位于同一直线上，两颗星围绕中央星在同一半径R的圆轨道上运行。设每个星体的质量均为m。试求这种形式下星体运动的线速度。 错解1：对做圆周运动的星体有  ，可得 ；错解2：  ，可得 。错因分析：上述解法的主要问题是对星体受力分析不全面导致错误，实际上每个星体都受到其它两个星体的引力作用，引力的合力提供向心力。 正解：由牛顿第二定律有：  ，解得： 。误区4：误认为地面上物体受的万有引力等于向心力 例4．已知同步卫星离地心距离为r，向心加速度为a1，地球赤道上的物体随地球自转的向心加速度为a2，地球的半径为R，则  为多少？错解：设地球质量为M，同步卫星质量为m  ，地球赤道上的物体质量为m ，根据万有引力定律有： ， 。联立解得： 。错因分析：卫星受到的万有引力全部提供向心力；而地面上物体运动的向心力不等于万有引力，向心力只是万有引力的一个分力，地球对物体的万有引力和支持力的合力提供向心力．对同步卫星有 ；而对赤道上的物体，有 （其中F =m2g）。正解：根据物体和同步卫星具有相同的角速度，有  ， ， ，解得 。误区5：弄不清“地上受阻减速”与“天上受阻变轨” 例5．某人造卫星运动的轨道可近似看作是以地心为中心的圆．由于阻力作用，人造卫星到地心的距离从r1慢慢变到r2，用EKl、EK2分别表示卫星在这两个轨道上的动能，则（ ） A．r1<r2，EK1<EK2 B．r1>r2，EK1<EK2 C．r1<r2，EK1>EK2 D．r1>r2，EK1>EK2 错解：由于阻力作用卫星的速度会减小，即v1>v2，速度减小，动能减小；由公式  知v变小，r变大，有r1<r2。故选Ｃ。 错因分析：当天体的速度发生变化时，卫星会做变轨运动（减速近心，加速离心），轨道半径会发生变化，向心加速度、线速度、角速度和周期也会连锁变化，可根据公式  ，， ， 判断其变化。正解：当卫星受到阻力的作用时，其速度会瞬时减小，假设此时卫星的轨道半径r还未变化，则由公式  可知卫星所需要的向心力减小；而此时卫星所受地球引力不变，有 > ，卫星必然会做向心运动而使轨道半径r变小，即r1>r2，由公式知变轨后卫星速度变大，动能变大即EK1<EK2（增加的动能由势能转变来的）。正确答案选B。误区6：混淆“地面追及”与“空间站对接” 例6．继2010年10月成功发射“嫦娥二号”，我国又于2011年9月发射“天宫一号”目标飞行器，2011年11月发射“神舟八号”飞船并与“天宫一号”成功实现对接，此后将要有航天员在轨进行科研，这在我国航天史上具有划时代意义。若某时刻“天宫一号”与“神舟八号”一前一后在同一轨道上做匀速圆周运动，“神舟八号”为了追上“天宫一号” 并实现成功对接，下列说法正确的是（ ） A．直接加速 B．先加速后减速 C．先减速后加速 D．选项B和C两种方法均可 错解：A、B、C、D四个选项均有同学错选。 错因分析：在太空中，飞行器之间的对接，不同于地面上直线运动物体的“追及”问题，必须明确飞行器由于变速会发生变轨现象。若两者在同一轨道上一前一后运动时要成功对接，不能仅靠某飞行器的单一变速实现。 正解：“神舟八号”加速，v增大，所需向心力 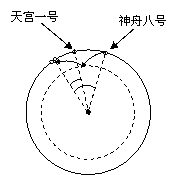 增大，加速瞬间 > ，引力不足以提供向心力，“神舟八号”做离心运动，无法实现对接，A选项错误。要实现对接，“神舟八号”在相同的时间内必须转过比“天宫一号”更大的角度，由公式可知在低轨道上的角速度更大，所以“神舟八号”必须先减速到低轨道后再加速才能成功对接，如图所示。故C选项正确。 
(责任编辑：admin) |