|
利用“实例”“推导”进行功的概念释疑 湖北省武汉市黄陂区第一中学 朱木清 “功”的概念，理论性强，应用性广，学生疑惑也多。如何释疑，至关重要。教学中，如果片面追求节省时间，以“超纲”为由回避矛盾，学生疑惑未解，达不到教学目的；偏于理论讲解，强行硬塞，脱离中学实际，不能消化。笔者认为，基于中学教学要求，为避免理论演绎抽象难懂，可采取“实例”的方式，借助具体模型理解领会；为弥补定性阐述不能满足学生“深入探究”需求的缺陷，可基于已有知识进行“推导”，定量求算证明。下面，以笔者的教学尝试，举例说明（注：问题选自学生的提问）。 1.合外力的功与外力功的总和是否相等？ 例1．如图1所示，甲、乙两小车的质量相等，用轻弹簧将两车连接，静止在光滑水平面上。现在同时对甲、乙两车施加等大反向的水平恒力F1、F2，使两车同时由静止开始运动，直到弹簧被拉到最长(弹簧仍在弹性限度内)的过程中，下列说法正确的是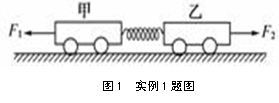（ ）  A．对两车及弹簧组成的系统，所受的合外力为零 B．对两车及弹簧组成的系统，外力对系统做功的总和为零 C．两车动能最大时，弹簧的弹力大小等于外力F1、F2的大小 D．两车的速度减小到零时，弹簧的弹力大小等于外力F1、F2的大小 解析：内力和外力称谓，是相对研究对象而言的。对两车及弹簧组成的系统，水平方向上，力F1、F2是外力，弹簧弹力是内力，故系统的合外力  =F1-F2=0，选项A对。对每个小车，合外力则由其一拉力和弹簧弹力组成。从小车静止到弹簧被拉到最长的过程中，弹簧弹力一直增大，小车的合力是先减小后反向增大，加速度先减小后反向增大，速度先增后减；当弹簧弹力增到与拉力等大时，合力与加速度为零，速度最大；当小车的速度减小到零时，合力与加速度同时达到最大。两车的运动具有对称性，类似于中点固定的弹簧振子，故选项C对，D错。再讨论外力的功：对单质点，可以证明：合外力做的功等于各力功的总和。但对质点系，“合外力的功”与“外力功的总和”意义就不同了。对两车及弹簧组成的系统，合外力 =0 ，“合外力的功”·s·cosα=0，而“外力功的总和”是W1+W2=F1s1+F2s2≠0，二者不等，选项B错误。故本题答案是：AC。这里摒弃纯理论演绎，用一个很平常的模型实例，把两种说法区分开来，学生易于接受，理解轻松愉悦。 2.是否存在两力做的总功等于这两力功“矢量和”的结论？ 例2．一运动物体从某时刻起受到两个互相垂直、大小分别为F1和F2的恒力作用，经一段时间后，在这两个力的方向上发生的位移大小分别为s1和s2，则在这段时间内这两个力对物体做的总功为（ ） A．（F1+F2）(s1+s2) B．F1s1+F2s2 C．  D． 解析：功是标量，过程总功等于各力功的代数和。学生可猜出选项B正确，但选项D错在哪，并不明白。这时，分析受力和运动情况，由于物体的初速度不为零，所受合力F（=  ）与初速度方向关系未知，故物体的合力F（=）与合位移s（= ）方向并不一定相同，作出矢量图示，如图2所示，由功的定义式，合力F与合位移s的夹角余弦不等于1，故选项D错误。本题正确答案：B。 再进一步推证：设F1与合力F的夹角为θ1，分位移s1与合位移s夹角为θ2，合力F与合位移s的夹角为α，则cosθ1=  ，sinθ1= ；cosθ2= ，sinθ2= ；α=θ1-θ2则F1做的功为W1=F1scosθ2=F1s1；F2做的功为W2=F2scos（90o-θ2）=F2s2；合力F做的功为W=Fscosα=Fscos(θ1-θ2)= Fs(cosθ1 cosθ2+sinθ1 sinθ2)= Fs( ·+·)= F1s1+ F2s2= W1+ W2。到此，学生懂了：该过程中这两力的总功等于两力功的代数和，而不存在什么“两力做的总功等于这两力功的‘矢量和’”结论。 3．功的数值与参考系的选择有关，是否因此会影响问题的答案？ 例3．如图3所示，一长度为L的木块固定在水平传送带上，随传送带一起以速度u匀速运动。质量为m可视质点的子弹，以一定的水平速度击中木块，受到的阻力恒为f，求子弹刚能击穿木块的初速度v0=？   解析：若以地面为参考，木块刚好被击穿，子弹的末速度和传送带速度相同，根据动能定理和牛顿定律有：-f(L+ut)=  m(u2-v02)，-f=ma=m ，即-ft=mu-mv0联立解得：v0=  +u由于木块和传送带一起匀速运动，是惯性系。若以木块和传送带为参考，子弹的初速度为（v0-u），刚好打穿木块时速度减为0，根据动能定理有：-fL=0- m(v0-u)2解得：v0= +u，结果同上。谜底揭晓，学生心里的“疙瘩”也消了：功能关系和动能定理成立的参考系是惯性系。选择不同的惯性系，动能定理都适用。尽管功和能的数值跟参考系选择有关，但不会影响所求问题的答案。 4．一对相互作用力的总功跟参考系选择有关吗？ 例4．如图4，倾角为θ的光滑斜劈M，停放在光滑水平地面上，物体m从斜劈上离地h高处释放后由静止开始滑下，物体m对斜劈M的压力N做正功，斜劈M对物体m的支持力N/做负功，求这一对相互作用的弹力所做的总功。   解析：所有接触面光滑，从能的转化角度容易理解：物体m下滑，其机械能的减少量应等于斜劈M机械能的增加量，系统总的机械能守恒，故应有这一对相互作用的弹力的功等值异号，代数和为零。但学生不满足：能否根据功的定义加以证明？故有必要往前再走一步。 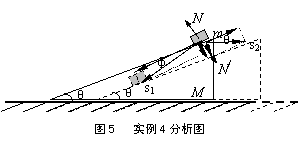  选地面为参考，设物体和斜劈相对地面的位移分别为s1和s2，如图5所示，s1与斜面夹角为φ，s2与斜面夹角应等于θ，则在垂直斜面方向上，二者的分位移相等，得：  ，弹力N对物体m做的功为： ，弹力N//对斜劈M做的功为 ，根据牛顿第三定律N=N/联立解得：  若选斜劈为参考，这对相互作用的弹力N和N/都不做功，总功为零。可见，选择不同参考系，这对相互作用的弹力的总功数值相同。 例5．如图6所示，质量为M的平板车停在光滑水平地面上，将质量为m的电动玩具车放在平板车上。开启玩具车电源，玩具车和平板车在水平方向上相互作用力大小为F，玩具车轮在平板车上无滑滚动，忽略电动玩具车内机件传动的能量损耗，当玩具车在平板车上前进距离s时，以下说法正确的有（ ）   A．电动玩具车获得动能为Fs B．平板车获得的动能为  FsC．一对水平相互作用力所做的总功为Fs D．两车获得的总动能为Fs 解析：以地面为参考，设电动玩具车向右的位移为s1，平板车往左的位移大小为s2，因相互作用力F/=F,对电动玩具车，有s1= a1t2= t2；对平板车有s2=a2t2=t2,故得： 。又s1+s2=s，所以s1=s，s2=s。根据动能定理，对电动玩具车，△Ek1=Fs1= Fs；对平板车，△Ek2=F/s2=Fs，故选项A错，B对。对系统△Ek1+△Ek2=Fs，选项D对。水平方向上， 这对相互作用力所做的总功为W1+W2= Fs1+ F/s2=F(s1+s2)= Fs,选项C对。故本题答案为：BCD 若选平板车为参考，玩具车对平板车的水平作用力F/的着力点不断变动，但受力点没有发生位移，故力F/不做功，w1/=0；玩具车所受作用力F做功W2/=Fs，故总功为W总/= w1/+ W2/=Fs。 由例4和例5可见：一对相互作用力的总功，是对系统内能量转化和转移的量度。例4中一对相互作用的弹力所做的总功为零，表明机械能只在系统内转移，没有转化为其它形式，系统机械能守恒；例5中，一对水平相互作用力所做的总功等于 Fs，正是电动机释放的能量为Fs，转化为系统的动能，系统机械能增加。电动机释放的能量是一定的，不因参考系选择而异，这与一对相互作用力的总功跟参考系选择无关相一致。明白了这点，为拓展学习质点系的动能定理，分析人体内力做功等质点系问题，大有帮助。 结语：借助“实例”释疑，顺应了由具体到抽象的学习认知规律；适时“推导”探究，体现了定性到定量的学科特点和教学要求。教学尝试表明，切合学生实际，易于接受理解。 参考文献： ［1］费宏。关于功的概念的争议与有关疑难问题的研究［J］。物理教师，2012，（10）：24 ［2］袁芳，朱炯明。功、动能和机械能［J］。 物理教学，2012，（7）：5 ［3］周长春，周钢。经典力学中功与能的相对性问题讨论［J］。 物理通报，2007,(12):17 (责任编辑：admin) |