|
第一章《三角函数》测试题 一、选择题 1.若角  的终边上有一点 ，则角的值可以是( ).A.  B. C. D. 考查目的：考查任意角三角函数的定义. 答案：A. 解析：因为  ，且 在第三象限，故 .2.下列函数中，最小正周期为  ，且图象关于直线 对称的是( ).A.  B. C. D. 考查目的：考查三角函数的图象和性质. 答案：C. 解析：∵最小正周期为 ，∴ ，又∵图象关于直线对称，∴ ，故只有C符合.3.函数  的部分图象如图，则 ， 可以取的一组值是( ).  A.  B. C.  D. 考查目的：考查函数 的图象与性质的灵活应用.答案：D. 解析：∵  ，∴ ， ，又由 得 .4.要得到  的图象，只需将 的图象( ).A.向左平移  个单位 B.向右平移个单位C.向左平移  个单位 D.向右平移个单位考查目的：考查三角函数图象的平移变换. 答案：C. 解析：∵  ，故选C.5.  为三角形 的一个内角，若 ，则这个三角形的形状为( ).A.锐角三角形 B.钝角三角形 C.等腰直角三角形 D.等腰三角形 考查目的：考查三角函数的性质和同角三角函数基本关系式的综合应用. 答案：B. 解析：将 两边平方，得 ，∴  .又∵ ，∴为钝角.6.设  为常数，且 ， ，则函数 的最大值为( ).A.  B. C. D. 考查目的：考查三角函数与二次函数性质的综合应用. 答案：B. 解析：  ，∵  ，∴ .又∵，∴ .二、填空题 7.在扇形中，已知半径为  ，弧长为 ，则圆心角是________弧度，扇形面积是_______.考查目的：考查扇形的弧长公式和面积公式. 答案：  ，48.解析： 圆心角  ，扇形面积 .8.函数  的最大值为________.考查目的：考查余弦函数的有界性、分式型函数值域的求法及转化化归思想. 答案：3. 解析：由  得 ，∴ ，解得 .9.函数  的单调递减区间是________.考查目的：考查正弦函数的单调性、周期性. 答案：  .解析：由  得 .10.已知函数  ，其中为实数，若 对 恒成立，且 ，则 的单调递增区间是________.考查目的：考查三角函数的图象和性质，以及分析和解决问题的能力. 答案：  .解析：由  对恒成立知， 或 .若，即 ，则 ，此时 ，矛盾，∴，∴ ，∴的单调递增区间是.11.给出下列命题： ①在  中，若 ，则 ；②在同一坐标系中，函数  与 的交点个数为2个；③将函数  的图象向右平移个单位长度可得到函数 的图象；④存在实数  ，使得等式 成立；其中正确的命题为________(写出所有正确命题的序号)． 考查目的：考查三角函数图象和性质的综合应用. 答案：①. 解析：②中两函数图象交点应为3个；③应向右平移  个单位长度得到的图象；④中 ，故只①对.三、解答题 12.已知 是第三角限角，化简 .考查目的：考查同角三角函数关系式的综合应用. 答案：  解析：∵ 是第三角限角，∴ ， ， ，∴    .13.已知角 的终边在直线 上，求角的正弦、余弦和正切值.考查目的：考查任意角三角函数的定义，及分类讨论思想. 答案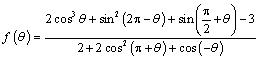：  ， ，2或 ， ，2.解析：设角 终边上任一点 ( )，则 ， ， .当  时， ，是第一象限角， ， ， ；当  时， ，是第三象限角， ， ，.综上，角 的正弦、余弦和正切值分别为，， 或，，14.⑴当  ，求 的值；⑵设  ，求 的值.考查目的：考查同角的三角函数关系式和三角函数的诱导公式. 答案：⑴ 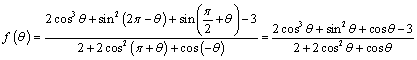 ；⑵ .解析：⑴∵  ，且，∴原式 ；⑵    ，∴ . 15.  已知函数 ， .⑴求函数 的最小正周期和单调递增区间；⑵求函数 在区间 上的最小值和最大值，并求出取得最值时的值.考查目的：考查三角函数的图象和性质. 答案：⑴ ， ；⑵最大值为 ，此时 ；最小值为 ，此时 .解析：⑴∵ ，∴函数的最小正周期为 .由  得 ，∴函数的递调递增区间为 ( )； ⑵∵ 在区间 上为增函数，在区间 上为减函数.又∵ ， ， ，故函数在区间上的最大值为，此时；最小值为，此时.(责任编辑：admin) |