高中期末考试越来越近了,鉴于数学知识点的重要性,小编为您提供了这篇双曲线方程知识点归纳总结,希望对同学们的数学有所帮助。
双曲线方程
1. 双曲线的第一定义:
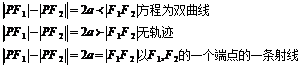
⑴①双曲线标准方程:
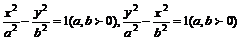
. 一般方程:
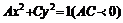
.
⑵①i. 焦点在x轴上:
顶点:
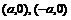
焦点:
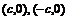
准线方程
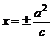
渐近线方程:
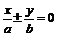
或
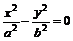
ii. 焦点在
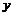
轴上:顶点:
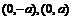
. 焦点:
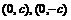
. 准线方程:
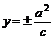
. 渐近线方程:
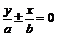
或
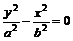
,参数方程:
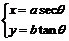
或
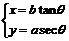
.
②轴
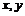
为对称轴,实轴长为2a, 虚轴长为2b,焦距2c. ③离心率
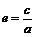
. ④准线距
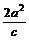
(两准线的距离);通径
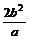
. ⑤参数关系
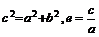
. ⑥焦点半径公式:对于双曲线方程
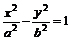
(
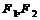
分别为双曲线的左、右焦点或分别为双曲线的上下焦点)
“长加短减”原则:

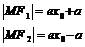
构成满足

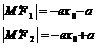
(与椭圆焦半径不同,椭圆焦半径要带符号计算,而双曲线不带符号)
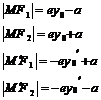
⑶等轴双曲线:双曲线
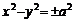
称为等轴双曲线,其渐近线方程为
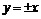
,离心率
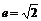
.
⑷共轭双曲线:以已知双曲线的虚轴为实轴,实轴为虚轴的双曲线,叫做已知双曲线的共轭双曲线.
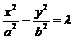
与
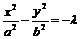
互为共轭双曲线,它们具有共同的渐近线:
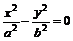
.
⑸共渐近线的双曲线系方程:
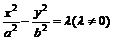
的渐近线方程为
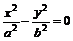
如果双曲线的渐近线为
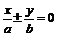
时,它的双曲线方程可设为
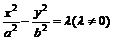
.
例如:若双曲线一条渐近线为
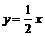
且过
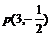
,求双曲线的方程?
解:令双曲线的方程为:
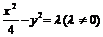
,代入
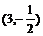
得
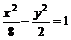
.
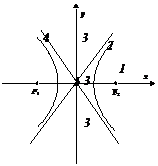
⑹直线与双曲线的位置关系:
区域①:无切线,2条与渐近线平行的直线,合计2条;
区域②:即定点在双曲线上,1条切线,2条与渐近线平行的直线,合计3条;
区域③:2条切线,2条与渐近线平行的直线,合计4条;
区域④:即定点在渐近线上且非原点,1条切线,1条与渐近线平行的直线,合计2条;
区域⑤:即过原点,无切线,无与渐近线平行的直线.
小结:过定点作直线与双曲线有且仅有一个交点,可以作出的直线数目可能有0、2、3、4条.
(2)若直线与双曲线一支有交点,交点为二个时,求确定直线的斜率可用代入
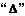
法与渐近线求交和两根之和与两根之积同号.
⑺若P在双曲线
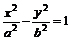
,则常用结论1:P到焦点的距离为m = n,则P到两准线的距离比为m︰n.
简证:
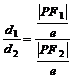
=
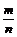
.
常用结论2:从双曲线一个焦点到另一条渐近线的距离等于b.
这篇双曲线方程知识点归纳总结,是精品小编精心为同学们准备的,祝大家学习愉快!
(责任编辑:admin) |