|
《1.2 应用举例（2）》测试题 一、选择题 1.有一长为  米的斜坡，它的坡度为 ，公路建设部门根据要求需要在坡底填土，使斜坡的坡度变为 ，则坡底将伸长( ).A. 米 B. 米 C. 米 D. 米考查目的：考查正弦定理、二倍角正弦公式的基本应用. 答案：D. 解析：如图，原斜坡为 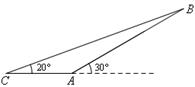 ，填土后的斜坡为 ，要求 的长. 根据题意可知， ， ， ，根据正弦定理得 ，∴ . 2.(2010北京文)某班设计了一个八边形的班徽(如图)，它由腰长为1，顶角为  的四个等腰三角形，及其底边构成的正方形所组成，该八边形的面积为( ). A.  B. C.  D. 考查目的：考查三角形面积公式、直角三角形边角关系或余弦定理，以及三角恒等变形能力. 答案：A. 解析：根据已知条件，四个等腰三角形的面积之和为  ，由直角三角形的边角关系得正方形的边长为 ，所以该八边形的面积为  .3.(由2009浙江文改编)在  中，角 所对的边分别为 ，且满足 ，若 ．则的面积为( ).A.  B. C. D. 考查目的：考查二倍角余弦公式、同角三角函数的基本关系式、三角形面积公式、向量的数量积以及运算求解能力. 答案：C. 解析：∵ ，∴ ，又∵ ，∴ ，而 ，∴ ，∴的面积为 .二、填空题 4.(2011上海理)在相距2千米的  两点处测量目标 ，若 ， ，则 两点之间的距离是 千米.考查目的：考查三角形内角和定理、正弦定理的应用. 答案：  .解析：根据三角形内角和定理得，  ，∴由正弦定理得 ，∴ .5.三角形的一边长为  ，这条边所对的角为 ，另两边之比为 ，则这个三角形的面积为 .考查目的：考查余弦定理及三角形面积公式. 答案：  .解析：不妨设 的边 ， ， ，则由余弦定理得 ，两式联立解得 ， ，∴ .6.我舰在岛  南偏西 方向相距 的 处发现敌舰正从岛沿北偏西 的方向以每小时 的速度航行，若我舰要用小时追上敌舰，则我舰追击的速度为 ，方向为 (精确到 ). 考查目的：考查正弦定理、余弦定理以及方程思想的应用. 答案：  小时，北偏东 .解析：设我舰以速度  航行，在处追上敌舰. 在中，由题意知 ， ， ， ，所以根据余弦定理得 ， ，∴ .设我舰追击的方向为北偏东角度，由正弦定理得 ， ，∴ ，故 .三、解答题： 7.(2008上海)如图，某住宅小区的平面图呈扇形  ．小区的两个出入口设置在点及点处，小区里有两条笔直的小路 ， ，且拐弯处的转角为 ．已知某人从沿 走到 用了 分钟，从沿 走到用了 分钟．若此人步行的速度为每分钟 米，求该扇形的半径 的长(精确到1米)． 考查目的：考查利用余弦定理解决实际问题的能力以及运算求解能力. 答案：  米解析：(方法一)设该扇形的半径为  米. 由题意，得 米， 米， .在 中， 即 ，解得 (米).(方法二)连接 ，作 ，交于 ，由题意，得米，米， ，在 中，   ，∴ 米.  .在直角 中， (米)， ，∴  (米).  8.在 中，的对边分别为，为 边上的高，且 ，试求 的最大值.考查目的：考查余弦定理、三角形面积公式、三角函数的恒等变形和性质以及运算求解能力. 答案：  .解析：由余弦定理，得  . 两边同除以 ，得 .∵ ，∴ ，即 ，代入上式得  ，(其中 为锐角，且 )，∴的最大值为.(责任编辑：admin) |