|
3.5不等式单元测试 1．设  ， ，则下列不等式中一定成立的是 （ ）A．  B． C． D． 2． “  ”是“ ”的 （ ）A．充分而不必要条件 B．必要而不充分条件 C．充要条件 D．既不充分也不必要条件 3．不等式  的解集不可能是 （ ） A．  B． C． D． 4．不等式  的解集是 ，则 的值等于 （ ）A．－14 B．14 C．－10 D．10 5．不等式  的解集是 （ ）A．  B． C．  或 D． 6．若  ，则下列结论不正确的是 （ ）A．  B． C． D． 7．若  ， ，则 与 的大小关系为 （ ）A．  B． C． D．随x值变化而变化8．下列各式中最小值是2的是 （ ） A．  ＋ B． C．tanx＋cotx D．  9．下列各组不等式中，同解的一组是 （ ） A．  与 B． 与 C．  与 D． 与 10．如果  对任意实数x总成立,则a的取值范围是 （ ）A.  B.  C.  D.  11．若  ，则 与 的大小关系是 .12．函数  的定义域是 .13．某公司一年购买某种货物400吨，每次都购买  吨，运费为4万元/次，一年的总存储费用为 万元，要使一年的总运费与总存储费用之和最小，则 吨.14. 已知  , 则不等式 的解集___ _ ____.15．已知 是奇函数，且在（－ ，０）上是增函数， ，则不等式 的解集是___ _ ____.16．解不等式：  17．已知  ，解关于的不等式 ．18．已知  ，求证： 。19．对任意  ，函数 的值恒大于零，求的取值范围。20．如图所示，校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。已知喷水器的喷水区域是半径为5m的圆。问如何设计花坛的尺寸和两个喷水器的位置，才能使花坛的面积最大且能全部喷到水？  21．已知函数  .（1）若对任意的实数 ，都有 ，求 的取值范围；（2）当  时，的最大值为M，求证： ；（3）若  ，求证：对于任意的， 的充要条件是 参考答案： 1.C; 2.A; 3.D; 4.C; 5.C; 6.D; 7.A; 8.D; 9.B; 10.A;11.  ; 12. ; 13. 20 ; 14.  ;15． ; 16．解：原不等式等价于：   或 ∴原不等式的解集为  17．解：不等式 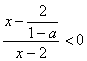可化为 ．∵ ，∴ ，则原不等式可化为 ，故当  时，原不等式的解集为 ；当  时，原不等式的解集为；当  时，原不等式的解集为 ．18．证明：法一（综合法）  ，  展开并移项得：   法二（分析法） 要证  ，，故只要证 即证  ，也就是证  ，而此式显然成立，由于以上相应各步均可逆，∴原不等式成立。 法三： ，  法四：   ， ∴由三式相加得：  两边同时加上 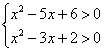 得： ， ∴19．解：设  ，则  的图象为一直线，在上恒大于0，故有 ，即 ，解得： 或 ∴ 的取值范围是 20．解：设花坛的长、宽分别为xm，ym，根据要求，矩形花坛应在喷水区域内，顶点应恰好位于喷水区域的边界。依题意得：  ，（ ）问题转化为在 ， 的条件下，求 的最大值。法一：  ，由  和及得：  法二：∵ ，， = ∴当  ，即 ， 由 可解得： 。答：花坛的长为  ，宽为 ，两喷水器位于矩形分成的两个正方形的中心，则符合要求。21． 解：（1）对任意的  ，都有 对任意的 ，   ∴ .（2）证明：∵   ∴ ，即。（3）证明：由  得， ∴在 上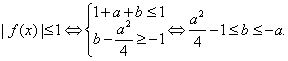是减函数，在 上是增函数。∴当  时,在 时取得最小值 ，在 时取得最大值 .故对任意的 ，  (责任编辑：admin) |