|
1.1正弦定理、余弦定理 重难点:理解正、余弦定理的证明,并能解决一些简单的三角形度量问题. 考纲要求:掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题. 经典例题:半径为R的圆外接于△ABC,且2R(sin2A-sin2C)=( (1)求角C; (2)求△ABC面积的最大值. 当堂练习: 1.在△ABC中,已知a=5, c=10, A=30°, 则∠B= ( ) (A) 105° (B) 60° (C) 15° (D) 105°或15° 2 (A) 30° (B) 45° (C) 60° (D) 75° 3.在△ABC中,已知三边a、b、c 满足(a+b+c)·(a+b-c)=3ab, 则∠C=( ) (A) 15° (B) 30° (C) 45° (D) 60° 4.边长为5、7、8的三角形的最大角与最小角之和为 ( ) (A) 90° (B) 120° (C) 135° (D) 150° 5.在△ABC中,∠A=60°, a=, b=4, 那么满足条件的△ABC ( ) (A) 有 一个解 (B) 有两个解 (C) 无解 (D)不能确定 6.在平行四边形ABCD中,AC=BD, 那么锐角A的最大值为 ( ) (A) 30° (B) 45° (C) 60° (D) 75° 7. 在△ABC中,若 (A) 等腰三角形 (B) 等边三角形 (C) 直角三角形 (D) 等腰直角三角形 8.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( ) (A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 由增加的长度决定 9.在△ABC中,若a=50,b=25, A=45°则B= . 10.若平行四边形两条邻边的长度分别是4cm和4cm,它们的夹角是45°,则这个平行四边形的两条对角线的长度分别为 . 11.在等腰三角形 ABC中,已知sinA∶sinB=1∶2,底边BC=10,则△ABC的周长是 。 12.在△ABC中,若∠B=30°, AB=2, AC=2, 则△ABC的面积是 . 13.在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足2sin(A+B)-=0,求角C的度数,边c的长度及△ABC的面积。 14.在△ABC中,已知边c=10, 又知==,求a、b及△ABC的内切圆的半径。 15.已知在四边形ABCD中,BC=a,DC=2a,四个角A、B、C、D度数的比为3∶7∶4∶10,求AB的长。 16.在△ABC中,已知角A、B、C所对的边分别是a、b、c,边c=,且tanA+tanB=tanA·tanB-,又△ABC的面积为S△ABC=,求a+b的值。 参考答案: 经典例题:解:(1)∵ ∴ 2R[( ∴ (2)∵ S= =- = 当堂练习: 1.D; 2.A; 3.D; 4.B; 5.C; 6.C; 7.B; 8.A; 9. 60°或120°; 10. 4cm和4cm; 11.50; 12. 2或; 13、解:由2sin(A+B)-=0,得sin(A+B)=, ∵△ABC为锐角三角形 ∴A+B=120°, C=60°, 又∵a、b是方程x2-2x+2=0的两根,∴a+b=2, a·b=2, ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6, ∴c=, S△ABC=absinC=×2×= . 14.解:由=,=,可得 =,变形为sinAcosA=sinBcosB ∴sin2A=sin2B, 又∵a≠b, ∴2A=π-2B, ∴A+B= 由a2+b2=102和=,解得a=6, b=8, ∴内切圆的半径为r===2 15、 解:设四个角A、B、C、D的度数分别为3x、7x、4x、10x,根据四边形的内角和有3x+7x+4x+10x=360°.解得 x=15° ∴A=45°, B=105°, C=60°, D=150° 连结BD,得两个三角形△BCD和△ABD 在△BCD中,由余弦定理得 BD2=BC2+DC2-2BC·DC·cosC=a2+4a2-2a·2a·=3a2, ∴BD=a.这时DC2=BD2+BC2,可得△BCD是以DC为斜边的直角三角形.∴∠CDB=30°, 于是∠ADB=120° 在△ABD中,由正弦定理有AB= 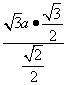 = =∴AB的长为 16、解:由tanA+tanB=tanA·tanB-可得 ∴tan(π-C)= -, ∴-tanC=-, ∴tanC=∵C∈(0, π), ∴C= 又△ABC的面积为S△ABC=,∴absinC= 即ab×=, ∴ab=6 又由余弦定理可得c2=a2+b2-2abcosC∴()2= a2+b2-2abcos ∴(a+b)2=, ∵a+b>0, ∴a+b= 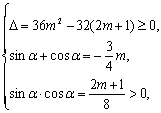 又 又 而2和 而2和(责任编辑:admin) |
