南昌市高中新课程训练题(不等式2)
命题人:南昌一中 喻瑞明
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若 ,则下列不等式成立的是( C ) ,则下列不等式成立的是( C )
A.? B. B. C. C.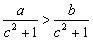 D. D.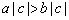
2.集合 、 、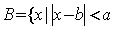 ,若 ,若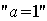 是 是 的充分条件,则B的取值范围可以是 ( ) 的充分条件,则B的取值范围可以是 ( )
A. B. B. C. C.  D. D.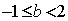
3.不等式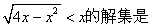 ( ) ( )
A.(0,2) B.(2,+∞) C. D. D.
4.设 ,函数 ,函数 则使 则使 的X的取值范围是( ) 的X的取值范围是( )
A. B. B.  C. C.  D. D. 
5.若2-m与|m|-3异号,则m的取值范围是 ( )
A. m>3 B.-3<m<3 C.2<m<3 D.-3<m<2 或m>3
6.设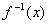 是函数 是函数 的反函数,则使 的反函数,则使 成立的x的取值范围为( ) 成立的x的取值范围为( )
A. B. B.  C. C.  D. D. 
7.不等式 的解集不是空集,则实数a的取值范围是( ) 的解集不是空集,则实数a的取值范围是( )
A. B. B. C. C. D. D.
8.设f(x)= 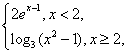  则不等式f(x)>2的解集为 ( ) 则不等式f(x)>2的解集为 ( )
A.(1,2) (3,+∞) B.( (3,+∞) B.( ,+∞) ,+∞)
C.(1,2) ( ( ,+∞) D.(1,2) ,+∞) D.(1,2)
9.a,b,u都是正实数,且a,b满足 ,则使得a+b≥u恒成立的u的取值范围是( ) ,则使得a+b≥u恒成立的u的取值范围是( )
A.(0,16) B.(0,12) C.(0,10) D.(0,8)
10.设 表示不大于x的最大整数,如:[ 表示不大于x的最大整数,如:[ ]=3,[—1.2]=-2,[0.5]=0,则使 ]=3,[—1.2]=-2,[0.5]=0,则使 ( ) ( )
A.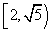 B. B.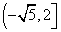 C. C. D. D.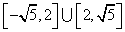
11.关于x的不等式x|x-a|≥2a2(a ( ) ( )
A. B. B. C. C. D.R D.R
12.在R上定义运算 ,若不等式 ,若不等式 成立,则( ) 成立,则( )
A.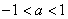 B. B. C. C. D. D.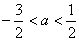
二、填空题:本大题共4小题,每小题4分,共16分。请把答案填在答题卡上。
13.某公司一年购买某种货物400吨,每次都购买 吨,运费为4万元/次,一年的总存储费用为 吨,运费为4万元/次,一年的总存储费用为 万元,要使一年的总运费与总存储费用之和最小,则 万元,要使一年的总运费与总存储费用之和最小,则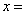 _________吨. _________吨.
14.若不等式  的解集为 的解集为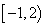  ,则a+b= 。 ,则a+b= 。
15.对a,b R,记max|a,b|= R,记max|a,b|= 函数f(x)=max||x+1|,|x-2||(x 函数f(x)=max||x+1|,|x-2||(x R)的最小值是 . R)的最小值是 .
16.关于 ,则实数k的值等于 。 ,则实数k的值等于 。
三、解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。
17.已知条件p:|5x-1|>a和条件 ,请选取适当的实数a的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题. ,请选取适当的实数a的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
18.解关于 的不等式 的不等式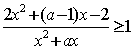
19.已知函数 有两个实根为 有两个实根为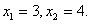
(1)求函数 ; ;
(2)设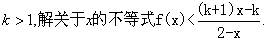
20.已知函数 的图象与x、y轴分别相交于点A、B、 的图象与x、y轴分别相交于点A、B、 (1)求 (1)求 ; ;
(2)当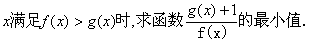
21.已知: 在 在 上是减函数,解关于 上是减函数,解关于 的不等式: 的不等式:

22.已知函数 为奇函数, 为奇函数,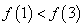 ,且不等式 ,且不等式 的解集是 的解集是 。 。
(1)求 的值; 的值;
(2)是否存在实数 使不等式 使不等式 对一切 对一切 成立?若存在,求出 成立?若存在,求出 的取值范围;若不存在,请说明理由。 的取值范围;若不存在,请说明理由。
参考答案
一、选择题
C D C AD,A C C A C ,B C
二、填空题
13.20 14.-2
15. 16. 16. 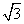
三、解答题
17.解:已知条件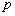 即 即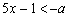 ,或 ,或 ,∴ ,∴ ,或 ,或 , ,
已知条件 即 即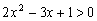 ,∴ ,∴ ,或 ,或 ; ;
令 ,则 ,则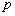 即 即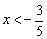 ,或 ,或 ,此时必有 ,此时必有 成立,反之不然. 成立,反之不然.
故可以选取的一个实数是 ,A为 ,A为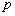 ,B为 ,B为 ,对应的命题是若 ,对应的命题是若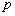 则 则 , ,
由以上过程可知这一命题的原命题为真命题,但它的逆命题为假命题.
18.解:原不等式可化为: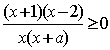
①当 时,原不等式的解集为 时,原不等式的解集为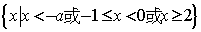
②当 时,原不等式的解集为 时,原不等式的解集为
③当 时,原不等式的解集为 时,原不等式的解集为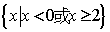
④当 时,原不等式的解集为 时,原不等式的解集为
⑤当 时,原不等式的解集为 时,原不等式的解集为
⑥当 时,原不等式的解集为 时,原不等式的解集为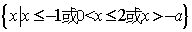
19.解:(1)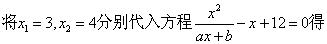
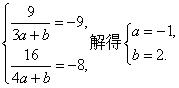
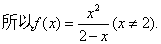
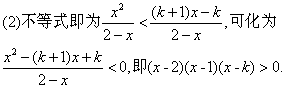
1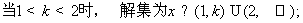
2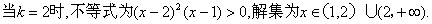
3
20.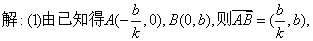
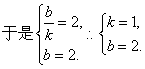

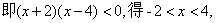
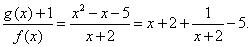
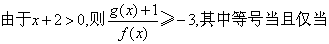
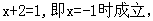

21. 解:由 得 得
由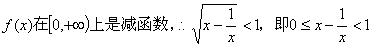
不等式的解集为
22.解:(1) 是奇函数 是奇函数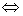 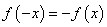 对定义域内一切 对定义域内一切 都成立 都成立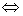 b=0,从而 b=0,从而 。又 。又 ,再由 ,再由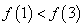 ,得 ,得 或 或 ,所以 ,所以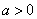 。 。
此时, 在 在 上是增函数,注意到 上是增函数,注意到 ,则必有 ,则必有 ,即 ,即 ,所以 ,所以 ,综上: ,综上: ; ;
(2)由(1), ,它在 ,它在 上均为增函数,而 上均为增函数,而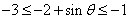 所以 所以 的值域为 的值域为 ,符合题设的实数 ,符合题设的实数 应满足 应满足 ,即 ,即 ,故符合题设的实数 ,故符合题设的实数 不存在。 不存在。
(责任编辑:admin) |
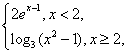
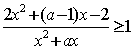
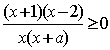

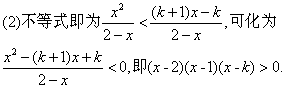
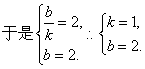

 ,再由
,再由