|
1.2正弦定理、余弦定理及其应用 考纲要求：能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题． 1. 有一长为1公里的斜坡，它的倾斜角为20°，现要将倾斜角改为10°，则坡底要伸长 （ ） A. 1公里 B. sin10°公里 C. cos10°公里 D. cos20°公里 2. 已知三角形的三边长分别为x2+x+1,x2－1和2x+1(x＞1)，则最大角为 （ ） A. 150° B. 120° C. 60° D. 75° 3．在△ABC中，  ，那么△ABC一定是 （ ）A．锐角三角形 B．直角三角形 C．等腰三角形 D．等腰三角形或直角三角形 4．在△ABC中，一定成立的等式是 ( ) A.asinA=bsinB B.acosA=bcosB C.asinB=bsinA D.acosB=bcosA 5．在△ABC中，A为锐角，lgb+lg(  )=lgsinA=－lg , 则△ABC为 （ ）A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 等腰直角三角形 6．在△ABC中，  ，则△ABC 的面积为 （ ）A.  B.  C.  D. 17．若  则△ABC为 （ ）A．等边三角形 B．等腰三角形 C．有一个内角为30°的直角三角形 D．有一个内角为30°的等腰三角形 8．边长为5、7、8的三角形的最大角与最小角之和的 （ ） A. 90° B. 120° C. 135° D. 150° 9．在△ABC中，根据下列条件解三角形，则其中有两个解的是 （ ） A．b = 10，A = 45°，B = 70° B．a = 60，c = 48，B = 100° C．a = 7，b = 5，A = 80° D．a = 14，b = 16，A = 45° 10．在三角形ABC中,已知A  ,b=1,其面积为 ,则 为 ( )A.  B.  C.  D.  11．某人站在山顶向下看一列车队向山脚驶来，他看见第一辆车与第二辆车的俯角差等于他看见第二辆车与第三辆车的俯角差，则第一辆车与第二辆车的距离  与第二辆车与第三辆车的距离 之间的关系为 （ ） A.  B.  C.  D. 不能确定大小12．在200米高的山顶上，测得山下一塔顶与塔底的俯角分别为30°、60°，则塔高为（ ） A.  米 B.  米 C. 200  米 D. 200米13. 在△ABC中，若  ， ， ，则 ．14. 在△ABC中，B=1350，C=150，a=5，则此三角形的最大边长为 . 15. 在锐角△ABC中，已知  ，则的 取值范围是 ．16. 在△ABC中，已知AB=4，AC=7，BC边的中线  ，那么BC= .17. 已知锐角三角形的三边长分别为2、3、  ，则的取值范围是 ．18. 在△ABC中，已知  ， ，则其最长边与最短边的比为 ．19．为了测量上海东方明珠的高度，某人站在A处测得塔尖的仰角为  ，前进38.5m后，到达B处测得塔尖的仰角为 .试计算东方明珠塔的高度（精确到1m）.20．在  中，已知 ，判定的形状．21.在△ABC中，最大角A为最小角C的2倍，且三边a、b、c为三个连续整数，求a、b、c的值. 22.在△ABC中，若  ，试求 的值．23． 如图，已知  的半径为1，点C在直径AB的延长线上，BC＝1，点P是上半圆上的一个动点，以PC为边作正三角形PCD，且点D与圆心分别在PC两侧. （1）若  ，试将四边形OPDC的面积y表示成  的函数；（2）求四边形OPDC面积的最大值. 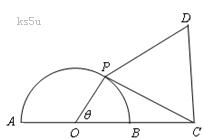 参考答案： 1.A; 2.B; 3.D; 4.C; 5.D; 6.C; 7.B; 8.B; 9.D; 10.B; 11.C; 12.A; 13．  14． 15． 16．9 17． 18． 19.468m 20.等腰三角形或直角三角形 21.a＝6，b＝5，c＝4 22.  23. (1) (2)2＋ w (责任编辑：admin) |