|
1.2回归分析 重难点：解聚类分析的基本思想、方法及其简单应用；了解回归的基本思想、方法及其简单应用． 考纲要求：①了解聚类分析的基本思想、方法及其简单应用． ②了解回归的基本思想、方法及其简单应用． 经典例题：某校医务室抽查了10名学生在高一和高二时的体重（单位：kg）如下表：
（1）利用相关系数r判断  与 是否具有相关关系？（2）若 与具有相关关系,试估计高一体重为78kg的学生在高二时的体重．当堂练习： 1.下列两个变量之间的关系中，哪个是函数关系 （ ） A.学生的性别与他的数学成绩 B.人的工作环境与健康状况 C.女儿的身高与父亲的身高 D. 正三角形的边长与面积 2．从某大学随机选取8名女大学生，其身高 (cm)和体重(kg)的回归方程为  ，则身高172cm的女大学生，由回归方程可以预报其体重 （ ）A.为6 0.316  B. 约为6 0.316 C.大于6 0.316 D.小于6 0.3163．为研究变量 和 的线性相关性，甲、乙二人分别作了研究，利用线性回归方法得到回归直线方程 和 ，两人计算知 相同， 也相同，则与的关系为 ( )A．重合 B.平行 C．相交于点  D. 无法判断4．设两个变量x和y之间具有线性相关关系，它们的相关系数是  ，关于的回归直线的回归系数为 ，回归截距是 ，那么必有 （ ） A． 与 的符号相同 B. 与的符号相同 C. 与的符号相反 D. 与的符号相反5. 工人月工资（元）依劳动生产率（千元）变化的回归直线方程为  ，下列判断正确的是 （ ）A．劳动生产率为1000元时，工资为340元 B．劳动生产率提高1000元时，工资提高180元 C．劳动生产率提高1000元时，工资平均提高180元 D.工资为520元时，劳动生产率为2000元 6．由右表可计算出变量  的线性回归方程为（ ）
A.  B.  C.  D.  7．若回归直线方程中的回归系数b=0时，则相关系数 = 8．下列结论中，能表示变量 具有线性相关关系的是 ①  ② ③ ④ 9．下列说法中正确的是 （填序号） ①回归分析就是研究两个相关事件的独立性；②回归模型都是确定性的函数；③回归模型都是线性的；④回归分析的第一步是画散点图或求相关系数 ；⑤回归分析就是通过分析、判断，确定相关变量之间的内在的关系的一种统计方法.10．变量 与具有线性相关关系，当取值为16,14,12,8时，通过观测得到的值分别为11,9，8，5.若在实际问题中，的预报最大取值是10，则的最大取值不能超过多少？11．在某年一项关于16艘轮船的研究中，船的吨位区间从192吨到3246吨，船员的数目从5人到32人.船员人数 关于船的吨位的线性回归方程为 (1)假设两艘轮船吨位相差1000吨，则船员平均人数相差多少？ (2)对于最小的船估计的船员数是多少？对于最大的船估计的船员数是多少？（本小题保留整数） 12．已知10只狗的血球体积及红血球的测量值如下（ｘ（血球体积，ｍｍ），ｙ（血红球数，百万））:
(1)画出上表的散点图； (2)求  ， ， ， ； （3）由散点图判断能否用线性回归方程来刻画与之间的关系，若能，求出线性回归方程.参考答案： 经典例题： (1)  ，    . 由小概率0.05及 查得 ∵  , ∴ 与具有相关关系.(2)  ， ∴ 回归直线方程为：  ，当 时， .即计高一体重为78kg的学生在高二时的体重约为81kg. 当堂练习： 1.D; 2.B; 3.C; 4.A; 5.C; 6.A; 7. 0; 8. ③; 9. ④⑤; 10．15. 11. （1）6.2人；（2）11人，30人. 12.（１）散点图如下图 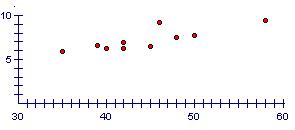 （２）    ， （3）由散点图知：能用线性回归方程来刻画 与之间的关系，设回归直线为     ∴ 线性回归方程为：  (责任编辑：admin) |