|
错解剖析得真知（三十三） 第十一章 数系的扩充与复数 §11.1 数系的扩充与复数的概念 一、知识导学 1. 复数：形如  的数（  ），复数通常有小写字母 表示，即 ,其中 叫做复数的实部、 叫做复数的虚部， 称做虚数单位.2. 分类：复数 ()中，当 时，就是实数；除了实数以外的数，即当b 时，叫做虚数；当 ,b时，叫做纯虚数.3. 复数集：全体复数所构成的集合. 4. 复数相等：如果两个复数 与 的实部与虚部分别相等，记作：=.5. 复平面、实轴、虚轴：建立直角坐标系来表示复数的平面.在复平面内，  轴叫做实轴， 轴叫做虚轴.6. 复数的模：设  =,则向量的长度叫做复数的模（或绝对值），记作 .(1)  ；(2)  = ；(3)  ；7．共扼复数：如果两个复数的实部相等，而虚部互为相反数，则这两个复数互为共扼复数. 二、疑难知识导析 1．两个实数可以比较大小，而不全是实数的两个复数不能比较大小 2．  则 ，而 ，则不一定成立，如 时 ；3．  ，而则 不一定成立；4．若   不一定能推出 ；5．若  ，则 = ，但若 则上式不一定成立.三、经典例题导讲 [例1]两个共扼复数的差是（ ）  .实数  .纯虚数  .零  .零或纯虚数错解:当得到  时就错误的选B，忽略了b可以为零的条件.正解：设互为共扼的两复数分别为 及 则 或 当  时， ， 为纯虚数当  时， ， ，因此应选D.注：要认真审题，看清题设条件，结论. 学会全面辩证的思考问题，准确记 忆有关概念性质. [例2]判断下列命题是否正确 (1)若 , 则(2)若  且 ，则 (3)若  ，则 错解：(1)认为任何一个实数的平方大于零可推广到复数中，从而(1)是正 确的 (2)认为两实数之差大于零等价于前一个大于后一个实数，也可推到复 数中来.认为两复数差为实数则这两个复数也为实数.而认为命题(2)是正确的. (3)把不等式性质错误的推广到复数中，忽略不等式是在实数中成立的 前提条件. 正解：(1)错，反例设 则 (2)错，反例设  ， ，满足 ，但  不能比较大小. (3)错，  ， ，故 ， 都是虚数，不能比较大小.[例3]实数 分别取什么值时，复数 是(1)实数；(2)虚数;(3)纯虚数. 解：实部  ，虚部 .（1）当  时，是实数；（2）当  ，且 时，是虚数；（3） 当  或 时是纯虚数．[例4] 设  ，当 取何值时，(1)  ; (2) .分析：复数相等的充要条件，提供了将复数问题转化为实数问题的依据，这是解复数问题常用的思想方法，这个题就可利用复数相等的充要条件来列出关于实数  的方程，求出 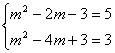的值．解：(1)由可得：  解之得 ，即：当  时 (2)当  可得： 或 ，即 时.[例5]  是两个不为零的复数，它们在复平面上分别对应点P和Q，且 ，证明△OPQ为直角三角形（O是坐标原点），并求两锐角的度数．分析 本题起步的关键在于对条件 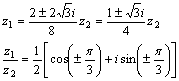的处理．等式左边是关于的二次齐次式，可以看作二次方程求解，也可配方．解：由 （ ，不为零），  得 即向量  与向量 的夹角为 ，在图中，  ，又 ，设 ，在△OPQ中，由余弦定理  △OPQ为直角三角形，  ．四、典型习题导练 1. 设复数z满足关系  ，那么z等于（ ）．A．  B． C． D． 2.复数系方程  有实数根，则这个实数是 .3. 实数m取何值时，复数  是(1)纯虚数；(2)在复平面上的对应点位于第二象限．4.已知  且 求复数.5.设复数 满足 且 在复平面上对应的点在第二象限、四象限的角平分线上， 求 的值.(责任编辑：admin) |