|
运用米勒定理简解最大角问题 湖北省阳新县高级中学 邹生书 1.米勒问题和米勒定理 1471年,德国数学家米勒向诺德尔教授提出了如下十分有趣的问题:在地球表面的什么部位,一根垂直的悬杆呈现最长?即在什么部位,视角最大?最大视角问题是数学史上100个著名的极值问题中第一个极值问题而引人注目,因为德国数学家米勒曾提出这类问题,因此最大视角问题又称之为“米勒问题”,更一般的米勒问题如下: 米勒问题:已知点 对米勒问题有如下重要结论我们不妨称之为米勒定理。 米勒定理:已知点 证明:如图1,设 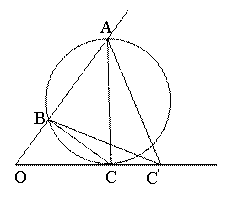 图1 根据切割线定理得, 2.米勒定理在解题中的应用 最大视角问题在数学竞赛、历届高考和模拟考试中频频亮相,常常以解析几何、平面几何和实际应用为背景进行考查。若能从题设中挖出隐含其中的米勒问题模型,并能直接运用米勒定理解题,这将会突破思维瓶颈、大大减少运算量、降低思维难度、缩短解题长度,从而使问题顺利解决。否则这类问题将成为考生的一道难题甚至一筹莫展,即使解出也费时化力。下面举例说明米勒定理在解决最大角问题中的应用。 2.1用米勒定理确定最大视角的点的位置 例1(1986年全国高考数学试题理科第五大题)如图2,在平面直角坐标系中,在 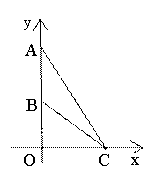 图2 分析:这是一道较早的“米勒问题”的高考题,该题背景简单解题思路入口宽解法多样,是一道难得的好题。若用米勒定理求解则可一步到位,轻而易举地拿下此题。 简解:设 例2 如图3,足球场长100米,宽60米,球门长7.2米,有一位左边锋欲射门,应在边 解:依题意  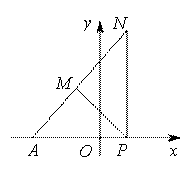 图3 图4  图5 例3(2004年全国数学竞赛试题)在直角坐标系中,给定两点 解:如图4,设直线 2.2用米勒定理探索最大视角的条件 例4(2010年高考江苏理科第17题)某兴趣小组要测量电视塔 (1)该小组已测得一组 (2)若该小组分析若干测得的数据后,认为适当调查整标杆到电视塔的中距离 解:(2)设 点评:第(2)问以实际应用和平面几何为背景考查最大角问题,本解法以米勒定理和相似三角形等知识为突破口,结合方程思想求解,综合性强能力立意高有一定难度。 2.3用米勒定理求最大视角或其三角函数值 例5(2001年希望杯数学竞赛培训题) 解:如图6,易求得  ,所以 ,所以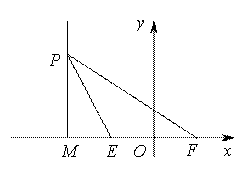 图6 更一般地我们有如下结论: 例6 设 证明:设准线交 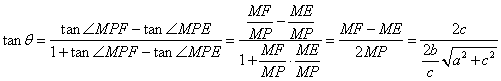 所以  。故 。故点评:由例6结论知,当 2.4用米勒定理求视角最大时有关线段之比 例7(2006年全国高中数学竞赛题)已知椭圆 解:如图7,设直线与  图7 易求得 点评:本解法不仅用到米勒定理的结论,而且还要熟悉定理证明的几何背景及图形间的内在联系,用相似三角形对应边成比例求线段比,运算量小解法简单快捷。 2.5用米勒定理求视角最大时的综合问题 例8 设 解:如图8,由米勒定理知,当且仅当 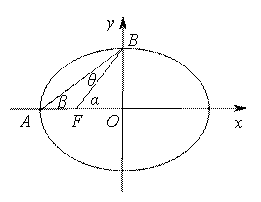 图8 即 设 则 所以 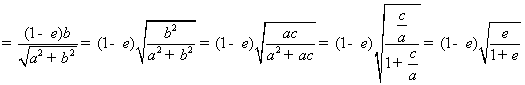 另外我们求最大角 点评:本题以椭圆为载体,重点考查椭圆的离心率等有关知识,考查三角公式、恒等变形和推理论证能力。本解法在求最大角的正弦值时需要很强的化归意识,即要有明确的化简目标,先把用 本文案例启发我们在平时的解题教学中,要引导学生进行解题反思,总结解题规律、揭示问题本质、提炼思想方法、归纳一般性结论,并有意识地加以运用,这样学生的解题能力定可上一级台阶达到较高的层次。 (责任编辑:admin) |
