|
高中数学竞赛讲义(十一) ──圆锥曲线 一、基础知识 1.椭圆的定义,第一定义:平面上到两个定点的距离之和等于定长(大于两个定点之间的距离)的点的轨迹,即|PF1|+|PF2|=2a (2a>|F1F2|=2c). 第二定义:平面上到一个定点的距离与到一条定直线的距离之比为同一个常数e(0<e<1)的点的轨迹(其中定点不在定直线上),即 第三定义:在直角坐标平面内给定两圆c1: x2+y2=a2, c2: x2+y2=b2, a, b∈R+且a≠b。从原点出发的射线交圆c1于P,交圆c2于Q,过P引y轴的平行线,过Q引x轴的平行线,两条线的交点的轨迹即为椭圆。 2.椭圆的方程,如果以椭圆的中心为原点,焦点所在的直线为坐标轴建立坐标系,由定义可求得它的标准方程,若焦点在x轴上,列标准方程为 参数方程为 若焦点在y轴上,列标准方程为 3.椭圆中的相关概念,对于中心在原点,焦点在x轴上的椭圆 a称半长轴长,b称半短轴长,c称为半焦距,长轴端点、短轴端点、两个焦点的坐标分别为(±a, 0), (0, ±b), (±c, 0);与左焦点对应的准线(即第二定义中的定直线)为 椭圆有两条对称轴,分别是长轴、短轴。 4.椭圆的焦半径公式:对于椭圆 5.几个常用结论:1)过椭圆上一点P(x0, y0)的切线方程为 2)斜率为k的切线方程为 3)过焦点F2(c, 0)倾斜角为θ的弦的长为 6.双曲线的定义,第一定义: 满足||PF1|-|PF2||=2a(2a<2c=|F1F2|, a>0)的点P的轨迹; 第二定义:到定点的距离与到定直线距离之比为常数e(>1)的点的轨迹。 7.双曲线的方程:中心在原点,焦点在x轴上的双曲线方程为 参数方程为 焦点在y轴上的双曲线的标准方程为 8.双曲线的相关概念,中心在原点,焦点在x轴上的双曲线 a称半实轴长,b称为半虚轴长,c为半焦距,实轴的两个端点为(-a, 0), (a, 0). 左、右焦点为F1(-c,0), F2(c, 0),对应的左、右准线方程分别为 9.双曲线的常用结论,1)焦半径公式,对于双曲线 2) 过焦点的倾斜角为θ的弦长是 10.抛物线:平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线,点F叫焦点,直线l叫做抛物线的准线。若取经过焦点F且垂直于准线l的直线为x轴,x轴与l相交于K,以线段KF的垂直平分线为y轴,建立直角坐标系,设|KF|=p,则焦点F坐标为 11.抛物线常用结论:若P(x0, y0)为抛物线上任一点, 1)焦半径|PF|= 2)过点P的切线方程为y0y=p(x+x0); 3)过焦点倾斜角为θ的弦长为 12.极坐标系,在平面内取一个定点为极点记为O,从O出发的射线为极轴记为Ox轴,这样就建立了极坐标系,对于平面内任意一点P,记|OP|=ρ,∠xOP=θ,则由(ρ,θ)唯一确定点P的位置,(ρ,θ)称为极坐标。 13.圆锥曲线的统一定义:到定点的距离与到定直线的距离的比为常数e的点P,若0<e<1,则点P的轨迹为椭圆;若e>1,则点P的轨迹为双曲线的一支;若e=1,则点P的轨迹为抛物线。这三种圆锥曲线统一的极坐标方程为 二、方法与例题 1.与定义有关的问题。 例1 已知定点A(2,1),F是椭圆 [解] 见图11-1,由题设a=5, b=4, c= 所以3|PA|+5|PF|=3(|PA|+ 所以当且仅当P为AM与椭圆的交点时,3|PA|+5|PF|取最小值,把y=1代入椭圆方程得 例2 已知P, [证明] 记右准线为l,作PD 2.求轨迹问题。 例3 已知一椭圆及焦点F,点A为椭圆上一动点,求线段FA中点P的轨迹方程。 [解法一] 利用定义,以椭圆的中心为原点O,焦点所在的直线为x轴,建立直角坐标系,设椭圆方程: 所以点P的轨迹是以F,O为两焦点的椭圆(因为a>|FO|=c),将此椭圆按向量m=( 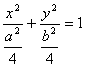 。由平移公式知,所求椭圆的方程为 。由平移公式知,所求椭圆的方程为 [解法二] 相关点法。设点P(x,y), A(x1, y1),则 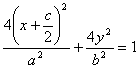 。它表示中心为 。它表示中心为例4 长为a, b的线段AB,CD分别在x轴,y轴上滑动,且A,B,C,D四点共圆,求此动圆圆心P的轨迹。 [解] 设P(x, y)为轨迹上任意一点,A,B,C,D的坐标分别为A(x- 当a=b时,轨迹为两条直线y=x与y=-x; 当a>b时,轨迹为焦点在x轴上的两条等轴双曲线; 当a<b时,轨迹为焦点在y轴上的两条等轴双曲线。 例5 在坐标平面内,∠AOB= [解] 设∠xOB=θ,并且B在A的上方,则点A,B坐标分别为B(3, 3tanθ),A(3,3tan(θ- 由外心性质知 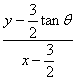 ×tanθ=-1。结合上式有 ×tanθ=-1。结合上式有又 tanθ+ 又 所以tanθ- 3.定值问题。 例6 过双曲线 [证明] 设点B,H,F的坐标分别为(asecα,btanα), (x0, 0), (c, 0),则F1,B1,B2的坐标分别为(-c, 0), (c, 所以 由①得 代入上式得  即 注:本例也可借助梅涅劳斯定理证明,读者不妨一试。 例7 设抛物线y2=2px(p>0)的焦点为F,经过点F的直线交抛物线于A,B两点,点C在准线上,且BC//x轴。证明:直线AC经过定点。 [证明] 设 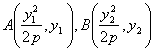 ,则 ,则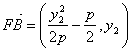 。由于 。由于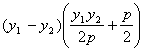 =0。因为 =0。因为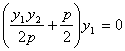 ,即 ,即例8 椭圆 [证明] 设|OA|=r1,|OB|=r2,且∠xOA=θ,∠xOB= 即 ①+②得 4.最值问题。 例9 设A,B是椭圆x2+3y2=1上的两个动点,且OA [解] 由题设a=1,b= 因为 例10 设一椭圆中心为原点,长轴在x轴上,离心率为 [解] 设A,B分别为圆C和椭圆上动点。由题设圆心C坐标为 因为 若 若t> 所以椭圆方程为 5.直线与二次曲线。 例11 若抛物线y=ax2-1上存在关于直线x+y=0成轴对称的两点,试求a的取值范围。 [解] 抛物线y=ax2-1的顶点为(0,-1),对称轴为y轴,存在关于直线x+y=0对称两点的条件是存在一对点P(x1,y1), 所以 例12 若直线y=2x+b与椭圆 [解] 二方程联立得17x2+16bx+4(b2-1)=0.由Δ>0,得 三、基础训练题 1.A为半径是R的定圆⊙O上一定点,B为⊙O上任一点,点P是A关于B的对称点,则点P的轨迹是________. 2.一动点到两相交直线的距离的平方和为定值m2(>0),则动点的轨迹是________. 3.椭圆 4.双曲线方程 5.椭圆 6.直线l被双曲线 7.ΔABC的三个顶点都在抛物线y2=32x上,点A(2,8),且ΔABC的重心与这条抛物线的焦点重合,则直线BC的斜率为________. 8.已知双曲线的两条渐近线方程为3x-4y-2=0和3x+4y-10=0,一条准线方程为5y+4=0,则双曲线方程为________. 9.已知曲线y2=ax,与其关于点(1,1)对称的曲线有两个不同的交点,如果过这两个交点的直线的倾斜角为450,那么a=________. 10.P为等轴双曲线x2-y2=a2上一点, 11.已知椭圆 12.已知(i)半圆的直径AB长为2r;(ii)半圆外的直线l与BA的延长线垂直,垂足为T,设|AT|=2a(2a< 13.给定双曲线 四、高考水平测试题 1.双曲线与椭圆x2+4y2=64共焦点,它的一条渐近线方程是 2.过抛物线焦点F的直线与抛物线相交于A,B两点,若A,B在抛物线准线上的射影分别是A1,B1,则∠A1FB1=_________. 3.双曲线 4.椭圆的中心在原点,离心率 5.4a2+b2=1是直线y=2x+1与椭圆 6.若参数方程 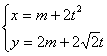 (t为参数)表示的抛物线焦点总在一条定直线上,这条直线的方程是_________. (t为参数)表示的抛物线焦点总在一条定直线上,这条直线的方程是_________.7.如果直线y=kx+1与焦点在x轴上的椭圆 8.过双曲线 9.过坐标原点的直线l与椭圆 10.以椭圆x2+a2y2=a2(a>1)的一个顶点C(0,1)为直角顶点作此椭圆的内接等腰直角三角形ABC,这样的三角形最多可作_________个. 11.求椭圆 12.设F,O分别为椭圆 13.已知双曲线C1: (1)求证:C1,C2总有两个不同的交点。 (2)问:是否存在过C2的焦点F1的弦AB,使ΔAOB的面积有最大值或最小值?若存在,求直线AB的方程与SΔAOB的最值,若不存在,说明理由。 五、联赛一试水平训练题 1.在平面直角坐标系中,若方程m(x2+y2+2y+1)=(x-2y+3)2表示的曲线为椭圆,则m的取值范围是_________. 2.设O为抛物线的顶点,F为焦点,且PQ为过F的弦,已知|OF|=a,|PQ|=b,ΔOPQ面积为_________. 3.给定椭圆 4.设F1,F2分别是双曲线 5.ΔABC一边的两顶点坐标为B(0, 6.长为l(l<1)的线段AB的两端点在抛物线y=x2上滑动,则线段AB的中点M到x轴的最短距离等于_________. 7.已知抛物线y2=2px及定点A(a,b),B(-a,0),ab≠0,b2≠2pa,M是抛物线上的点,设直线AM,BM与抛物线的另一个交点分别为M1,M2,当M变动时,直线M1M2恒过一个定点,此定点坐标为_________. 8.已知点P(1,2)既在椭圆 9.已知椭圆 10.设曲线C1: (2)O为原点,若C1与x轴的负半轴交于点A,当0<a< 11.已知直线l过原点,抛物线C的顶点在原点,焦点在x轴正半轴上,若点A(-1,0)和B(0,8)关于l的对称点都在C上,求直线l和抛物线的方程。 六、联赛二试水平训练题 1.在四边形ABCD中,对角线AC平分∠BAD,在CD上取一点E,BE与AC相交于F,延长DF交BC于G,求证:∠GAC=∠EAC。 2.求证:在坐标平面上不存在一条具有奇数个顶点,每段长都为1的闭折线,它的每个顶点坐标都是有理数。 3.以B0和B1为焦点的椭圆与ΔAB0B1的边ABi交于Ci(i=0,1),在AB0的延长线上任取点P0,以B0为圆心,B0P0为半径作圆弧 4.在坐标平面内,从原点出发以同一初速度v0和不同发射角(即发射方向与x轴正向之间 的夹角)α(α∈[0,π],α≠ 5.直角ΔABC斜边为AB,内切圆切BC,CA,AB分别于D,E,F点,AD交内切圆于P点。若CP 6.已知BC 本系列讲座由在人教中数论坛网友“0.1”整理提供,感谢他(她)的分享。 (责任编辑:admin) |
