|
1.1-2 算法的含义、程序框图 重难点： 通过实例体会算法的思想，了解算法的含义，了解算法的主要特点（有限性和确定性）；能用流程图表示顺序、选择、循环这三种基本结构，能识别简单的流程图所描述的算法． 考纲要求：①了解算法的含义、了解算法的思想． ②理解程序框图的三种基本逻辑结构：顺序、条件分支、循环． 经典例题：阅读下列伪代码，并指出当  时的计算结果：⑴read a, b (2) read a, b (3) read a, b X←a+b a←a+b a←a+b y←a-b b←a-b b←a-b a←(x+y)/2 a←(a+b)/2 a←(a-b)/2 b←(x-y)/2 b←(a-b)/2 b←(a+b)/2 Print a, b Print a, b Print a, b a= ，b= a= ，b= a= ，b= 当堂练习： 1．算法的有穷性是指（ ） A．算法必须包含输出 B．算法中每个操作步骤都是可执行的 C．算法的步骤必须有限 D．以上说法均不正确 2  用电水壶烧一壶开水，壶中还有一点儿水，若规定盖上水壶盖是最后一步，则插上电源是（ ）A．第二步 B．第三步 C．最后第二步 D．最后第三步 3．下列哪个不是算法的特征（ ） A．抽象性 B．精确性 C．有穷性 D．惟一性 4．以下给出的各数中不可能是八进制数的是（） A．312 B．10 110 C．82 D．7 457 5．下面对算法描述正确的一项是（ ）w.w.w.k.s.5.u.c.o.m A．算法只能用自然语言来描述 B．算法只能用图形方式来表示 C．同一问题可以有不同的算法 D．同一问题的算法不同，结果必然不同 6．下列各数中最小的数是（ ） A．  B． C． D． 7．算法共有三种逻辑结构，即顺序结构，条件结构和循环结构，下列说法正确的是（ ） A．一个算法只能含有一种逻辑结构 B．一个算法最多可以包含两种逻辑结构
n=0 while n<100 n=n+1 n=n*n wend print n end （第8题） A．5 B．4 C．3 D．9 9．计算机执行下面的程序段后，输出的结果是（ ） A．1，3 B．4，1 C．0，0 D．6，0 10．当  时，下面的程序段结果是（ ）w.w.w.k.s.5.u.c.o.mA．3 B．7 C．15 D．17 11．在一个算法中，算法的流程根据条件可以有几种不同的流向（ ） A．1 B．2 C．3 D．多于3个 12．对赋值语句的描述正确的是（ ） ①可以给变量提供初值 ②将表达式的值赋给变量 ③可以给一个变量重复赋值 ④不能给同一变量重复赋值 A．①②③ B．①② C．②③④ D．①②④ 13．给出以下四个问题, ①x, 输出它的相反数. ②求面积为6的正方形的周长.③求三个数a,b,c中输入一个数的最大数. ④求函数f(x)=  的函数值. 其中不需要用条件语句来描述其算法的有（ ）A．1个 B．2个 C．3个 D．4个 14．用秦九韶算法计算当x=5时多项式f (x)=5  +4 +3 +2 +x+1的值 ．15．一堆形状大小完全相同的珠子，其中只有一粒重量比其他的轻，某同学利用科学的算法，两次利用天平找出了这棵最轻的珠子，则这堆珠子至多有 粒． 16．用冒泡排序法从小到大排列数据{ 13，5，9 ，10，7，4 }，需要经过 趟排序才能完成． 17．循环结构描述算法，在画出算法流程图之前需要确定三件事：(1)确定循环变量和 ；(2)确定 ；(3)确定 ． 18．某电信部门规定：拨打市内电话时，如果通话时间不超过3分钟，则收取通话费0.2元，如果通话时间超过3分钟，则超过部分以每分钟0.1元收取通话费（通话不足1分钟时按1分钟计），试设计一个计算通话费用的算法.要求写出算法． 19．画出方程 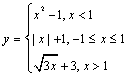 的根的流程图．20．设计算法求  的值.要求画出程序框图．21．已知函数  , 编写一程序求函数值．参考答案： 经典例题：3，5；3，－2.5；－5，1.5 当堂练习： 1.C; 2.C; 3.D; 4.C; 5.C; 6.D; 7.D; 8.B; 9.B; 10.C; 11.C; 12.A; 13.B; 14.18556; 15. 9; 16. 5; 17. 初始条件，循环体，终止条件; 18. 用c（单位：元）表示通话费，t（单位：分钟）表示通话时间， 则依题意有  算法步骤如下：第一步，输入通话时间t；第二步，如果t≤3,那么c = 0.2 ;否则令 c = 0.2+0.1 (t－3);第三步，输出通话费用c. 19.   20. 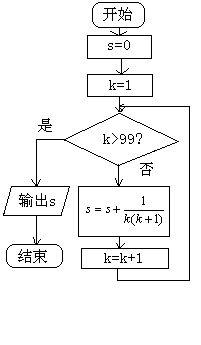  21.
 (责任编辑：admin) |