|
第二章《基本初等函数（Ⅰ）》测试题（二） 三、解答题 12.设  ，且 ，如果函数 在 上的最大值为14，求 的值.考查目的：考查指数的运算、指数函数的性质和二次函数在闭区间上的最值，以及转化化归思想. 答案：  或 .解析：令  ，则 .当 时， ， 在 时取得最大值，即 ，解得；当 时， ，在 时取得最大值，即 ，解得.综合以上两点得，或.13.已知对数函数  ，若对于任意的 都有 成立，试求 的取值范围.考查目的：考查对数函数图象与性质，以及数形结合思想和分类讨论思想. 答案：  .解析：函数 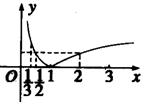 的图象如图所示.由图可知，要使对于任意的都有成立 ，只需 ，即 ，∴ ，变形得 ．当时， ；当时， . 综上所述， 的取值范围是.14.已知函数  ( ， ， ).⑴求  的定义域；⑵判断的奇偶性；⑶讨论的单调性，并证明．考查目的：考查函数的定义域与奇偶貹，以及复合函数的单调性的判断与证明. 答案：⑴  ；⑵奇函数；⑶当时，单调递减；当时，单调递增.解析：⑴解  得，函数的定义域为；⑵∵ ，∴为奇函数；⑶证明：设 ，则 ，  .当 时， ，∴在 上为减函数；同理在 上也为减函数；当时， ，∴在，上为增函数.15.(2012上海理20改编)已知函数  ．⑴若  ，求 的取值范围；⑵若  是偶函数， ，且当 时，有 ，求函数 ( )的解析式.考查目的：考查对数函数的性质、函数的概念与奇偶性、分段函数等基本知识，以及综合运用所学知识解决问题的能力. 答案：⑴  ；⑵ .解析：⑴由  得 .由即 ，得  ，即 ，解得 ，∴的取值范围是.⑵当  时， .∵当时，，∴ .又∵，∴ ，∴ .由是偶函数得，  ()，∴函数()的解析式为.(责任编辑：admin) |