|
2.5函数与方程 重难点：理解根据二次函数的图象与x轴的交点的个数判断一元二次方程的根的个数及函数零点的概念，对“在函数的零点两侧函数值乘积小于0”的理解；通过用“二分法”求方程的近似解，使学生体会函数的零点与方程根之间的关系，初步形成用函数观点处理问题的意识． 考纲要求：①结合二次函数的图像，了解函数的零点与方程根的联系，判断一元二次方程根的存在性及根的个数； ②根据具体函数的图像，能够用二分法求相应方程的近似解． 经典例题：研究方程|x2－2x－3|=a（a≥0）的不同实根的个数． 当堂练习： 1．如果抛物线f(x)= x2+bx+c的图象与x轴交于两点(-1,0)和(3,0),则f(x)>0的解集是（ ） A． (-1,3) B．[-1,3] C．  D．  2．已知f(x)=1-(x-a)(x-b)，并且m，n是方程f(x)=0的两根，则实数a,b,m,n的大小关系可能是（ ） A． m<a<b<n B．a<m<n<b C．a<m<b<n D．m<a<n<b 3．对于任意k∈［－1,1］,函数f(x)=x2+(k－4)x－2k+4的值恒大于零，则x的取值范围是 A．x<0 B．x>4 C．x<1或x>3 D．x<1 4． 设方程2x+2x=10的根为  ,则 （ ）A．(0,1) B．(1,2) C．(2,3) D．(3,4) 5．如果把函数y=f(x)在x=a及x=b之间的一段图象近似的看作直线的一段，设a≤c≤b，那么f(c)的近似值可表示为（ ） A．  B． C.f(a)+ D.f(a)－6．关于x的一元二次方程x2+2(m+3)x+2m+14=0有两个不同的实根,且一根大于3,一根小于1,则m的取值范围是 ． 7． 当a 时，关于x的一元二次方程 x2+4x+2a-12=0两个根在区间[-3,0]中． 8．若关于x的方程4x+a·2x+4=0有实数解，则实数a的取值范围是___________． 9．设x1,x2 分别是log2x=4-x 和2x+x=4的实根,则x1+x2= ． 10．已知  ,在下列说法中： (1)若f(m)f(n)<0,且m<n,则方程f(x)=0在区间(m,n)内有且只有一根； (2) 若f(m)f(n)<0,且m<n,则方程f(x)=0在区间(m,n)内至少有一根； (3) 若f(m)f(n)>0,且m<n,则方程f(x)=0在区间(m,n)内一定没有根； (4) 若f(m)f(n)>0,且m<n,则方程f(x)=0在区间(m,n)内至多有一根； 其中正确的命题题号是 ． 11．关于x的方程mx2+2(m+3)x+2m+14=0有两个不同的实根,且一个大于4,另一个小于4,求m的取值范围． 12．已知二次函数f(x)=a(a+1)x2-(2a+1)x+1,  ．（1）求函数f(x)的图象与x轴相交所截得的弦长； （2） 若a依次取1,2,3,4,---,n,时, 函数f(x)的图象与x轴相交所截得n条弦长分别为  求 的值．13． 已知二次函数  且满足  ．（1）证明：函数  的图象交于不同的两点A，B；（2）若函数  上的最小值为9，最大值为21，试求 的值；（3）求线段AB在  轴上的射影A1B1的长的取值范围．14．讨论关于x的方程lg(x-1)+lg(3-x)=lg(a-x)的实根个数． 参考答案： 经典例题：解：设y=|x2－2x－3|和y=a，利用Excel、图形计算器或其他画图软件，分别作出这两个函数的图象，它们的交点的个数，即为所给方程实根的个数．如下图，当a=0或a＞4时，有两个实根；当a=4时，有三个实根；当0＜a＜4时，有四个实根．  当堂练习： 1.C ; 2. A ; 3. C ;4. C ;5. C ; 6.  ; 7. ; 8.a≤－4; 9. 4; 10. (2);11.设f(x)= mx2+2(m+3)x+2m+14,根据图象知当  或 时,符合题意从而得  . 12. 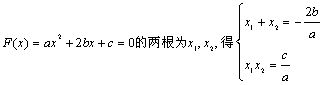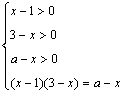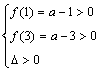（1）设抛物线与x轴相交于点(x1,0),(x2,0),则   ,得  ；（2）  = = 13.（1）由  ， 即函数的图象交于不同两点A，B；（2）  知函数F（x）在[2，3]上为增函数， （3）设方程    设  的对称轴为 上是减函数 14.解:原方程转化为  ,即方程x2-5x+a+3=0在区间（1,3）内是否有根,由 得: ,设f(x)= x2-5x+a+3,对称轴是 ,若 得有一根在区间（1,3）内,即当 时,原方程有一根; 若 得 时,原方程有两根;  时, 原方程无解．(责任编辑：admin) |