|
怎样思考解析几何问题的一题多解？ 我们举一个例子：已知两平行直线l1，l1的方程分别为3x＋2y－6＝0，6x＋3y＋3＝0。求与l1，l2平行且与它们等距离的直线l3的方程。 解法1：易知l1，l2分别与y轴相交于点  ，线段P1P2的中点为 ，所求直线l2经过点Q且与l1，l2平行，因此它的方程为 。解法2：设P(x，y)为直线l3上的任意一点，由点到直线的距离公式，得  化简即得12x＋8y－9＝0 。解法3（待定系数法）：由l1∥l2∥l3，可把l1的方程变形为6x＋4y－12＝0，且设l3的方程为6x＋4y＋c＝0 。观察这三个方程，只有常数项-12，c，3不同。不妨以c作为单个变量，那么根据l3是l1，l2的“正中平行线“，可得c与-12的距离等于c与3的距离，即|c＋12|＝|c－3|，解得  。因此l3的方程为 即12x＋8y－9＝0 。解法3是通法（待定系数法是通法，其中用到的知识也都是基础知识），又是妙法（巧妙地把x，y以为变量的坐标平面转化为以c为变量的直线，即把“二维”降为“一维”，运用了化归这一基本数学思想）。值得指出，为了同学们易于理解，笔者有意写得很详细。深谙此法的同学们往往只需写成“l1：6x＋4y－12＝0，l3：6x＋4y＋c＝0 =>|c＋12|＝|c－3| 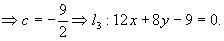 ”。(责任编辑：admin) |