|
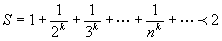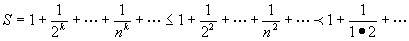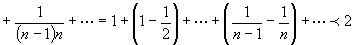怎样用逆证法和放缩法证明不等式？ （1）逆证法。这是分析法的一种特殊情况，即从要证明的不等式出发。寻找使这个不等式成立的某一既是“充分的“，又是“必需的”条件。如此逐步往前追溯，一直追溯到已知条件或一些真命题为止。逆证法的证明过程表现为一连串的“即”，可用一连串的“<=>”来代替，最后推至已知条件或真命题。 （2）放缩法。这也是分析法的一种特殊情况，它的根据是不等式的传递性—a≤b，b≤c，则a≤c，只要证明“大于或等于a的”b≤c就行了。例如证明当k是大于1的整数时，  ，我们可以用放缩法的一支——“逐步放大法”，证明如下：   有时要证a≥b，我们可以用放缩法的另一支——“逐步缩小法”，即证明a≥a1≥a2≥…≥an≥b 。放缩法在高等数学中经常使用，在中学仅供学有余力的同学研究。 (责任编辑：admin) |