|
西城教育研修学院中学数学室供稿 考试时间:100分钟 卷面总分:120分 注意:本卷中1-21题为模块考试试题,共100分;22、23题为非模块考试试题, 共20分. 一、选择题:本大题共14小题,每小题4分,共56分. 在每小题的4个选项中,只有一项是符合题目要求的. (1)设全集 A. C. (2)已知集合A={ A. (3)已知函数f (x) = A. R B.{x | x > 1} C.{x | x≠1} D.{x | x≠ (4)在下列各组函数中, A. C. (5)函数 A. R B. (6)设 A. (7)下列函数中为奇函数的是( ) A. y = C. y = x+1 D. y = (8)在同一坐标系中,函数y = A.关于y轴对称 .B.关于x轴对称 C.关于原点对称 .D.关于直线y = x对称 (9)下列函数中,在区间(0,+∞)上是增函数的是 ( ) A. y = x2 B. C. y = (9) (10) A. 9 B. (11)函数 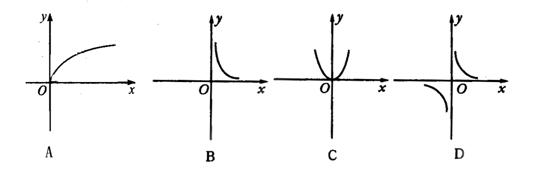 (12) 某种细胞分裂时,由1个分裂成2个,2个分裂成4个,4个分裂成8个,……如果 1个这样的细胞分裂后得到的细胞个数为32,那么分裂次数为( ) A.3 B.5 C.4 D.6 (13)已知 A. (14)一批价值1万元的设备,由于使用时磨损,每年比上一年价值降低5%,则2年后这批设备的价值为 ( ) A. 二、填空题:本大题共4小题,每小题4分,共16分.将答案填在题中横线上. 15.已知集合A={ 16.已知函数 17.函数 18.对于定义域为D的函数 的坐标为 . 三、解答题:本大题共5小题,共48分. 解答应写出文字说明、证明过程或演算步骤. 19.(本题10分) (1)计算 20.(本题10分) 已知函数 (1)点 (2)当 (3)当 21.(本题8分) 国庆“黄金周”及其前后是旅游旺季.某宾馆通过对9月26日至10月15日这20天的调查,得到部分日经济收入Q与这20天中的第
(1) 根据上表数据,从下列函数中选取一个最恰当的函数描述Q与 Q 并求出该函数的解析式; (2) 利用你选择的函数,确定日经济收入最高的是第几天;并求出最高日经济收入. 【本题为非模块考试题】 22. (本题10分)已知 (1) 求 (2) 求 (3) 若关于 【本题为非模块考试题】 23.(本题10分)已知 ( (1)求 (2)设 (3)设 函数 北京市朝阳区普通高中数学高一年级必修模块(一)试卷答案 一.选择题(每题4分) 1. A 2.D 3.B 4.D 5.C 6.C 7.D 8.A 9.A 10.C 11.A 12. B 13. A 14.D 二.填空题(每题4分) 15. 三.解答题 19.(10分每题5分) (1) 解:原式= 9-8+1 …………3分(每式1分) =2. …………5分 (2) 解:原式=2+(-1) …………4分(每式2分) =1. …………5分 20.(1)解:∵ ∴点(3,9)在函数 (2) (3)令 解得 ∴当 21.解:(1)由提供的数据知道,描述宾馆日经济收入Q与天数 将表格中提供的其中两组数据(1,218)、(8,288)代入 解得 所以 (2) ∵ ∴当 故日经济收入最高是第9天和第10天,最高日经济收入为290万元. …………8分 22.解:(1) (2) 设 即 (3)解法1: ∵函数 ∴只需考虑 即方程 ① 由 当 当 ② 由 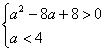 , ,∴ 综上所述, 解法2: 令 当 抛物线 依题意只有 结合图象知,当  的图象无交点,即方程 则当 23. 解: (1)∵ ∴ ∴ (2)当 当 ∴ 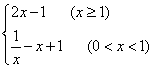 …………3分 …………3分则函数 下面证明: 设x1,x2是 则g (x1)- g (x2) 设x1,x2是(0,1)上的两个任意实数,且x1 < x2, 则g (x1)- g (x2) = = = 因为0<x1<x2<1,所以x2- x1 > 0,1+x1x2 > 0,x1x2 > 0. 所以g (x1) -g (x2) = 即g (x1) >g (x2). 所以 (3) 易知 (ⅰ)当 则 (ⅱ)当 (ⅲ) 综上所述, 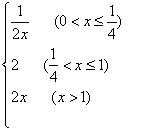 . …………9分 . …………9分根据分段函数 …………10分 注(3)问把解析式写为 (解答题如有不同解法,请酌情给分) 北京朝阳必修1模块考试题(08).zip (责任编辑:admin) |
