|
47、（广东文）在一个袋子中装有分别标注数字1，2，3，4，5的五个小球，这些小球除标注的数字外完全相同．现从中随机取出2个小球，则取出的小球标注的数字之和为3或6的概率是 A．  B． C． D． 【解答】随机取出2个小球得到的结果数有  种(提倡列举).取出的小球标注的数字之和为3或6的结果为 共3种,故所求答案为(A).48、（福建理）如图，三行三列的方阵中有9个数 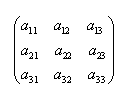 ，从中任取三个数，则至少有两个数位于同行或同列的概率是（ ） A．  B． C． D． 【解答】从中任取三个数共有  种取法，没有同行、同列的取法有 ，至少有两个数位于同行或同列的概率是 ，选D49、（福建理）两封信随机投入  三个空邮箱，则 邮箱的信件数 的数学期望 ． 【解答】ξ的取值有0，1，2，  ，所以Eξ= 50、（福建文）（本小题满分12分）甲、乙两名跳高运动员一次试跳  米高度成功的概率分别是 ， ，且每次试跳成功与否相互之间没有影响，求：（Ⅰ）甲试跳三次，第三次才成功的概率； （Ⅱ）甲、乙两人在第一次试跳中至少有一人成功的概率； （Ⅲ）甲、乙各试跳两次，甲比乙的成功次数恰好多一次的概率． 【解答】本小题主要考查概率的基础知识，运用数学知识解决问题的能力，以及推理与运算能力．满分12分． 记“甲第  次试跳成功”为事件 ，“乙第次试跳成功”为事件 ，依题意得 ， ，且，（ ）相互独立．（Ⅰ）“甲第三次试跳才成功”为事件  ，且三次试跳相互独立， ．答：甲第三次试跳才成功的概率为  ．（Ⅱ）“甲、乙两人在第一次试跳中至少有一人成功”为事件  ．解法一：  ，且 ， ， 彼此互斥，    ．解法二：  ．答：甲、乙两人在第一次试跳中至少有一人成功的概率为  ．（Ⅲ）设“甲在两次试跳中成功 次”为事件 ，“乙在两次试跳中成功 次”为事件 ， 事件“甲、乙各试跳两次，甲比乙的成功次数恰好多一次”可表示为 ，且 ， 为互斥事件， 所求的概率为     答：甲、乙每人试跳两次，甲比乙的成功次数恰好多一次的概率为  ．51、（北京理）（本小题共13分）某中学号召学生在今年春节期间至少参加一次社会公益活动（以下简称活动）．该校合唱团共有100名学生，他们参加活动的次数统计如图所示． （I）求合唱团学生参加活动的人均次数； （II）从合唱团中任意选两名学生，求他们参加活动次数恰好相等的概率． （III）从合唱团中任选两名学生，用 表示这两人参加活动次数之差的绝对值，求随机变量的分布列及数学期望 ．  【解答】解：由图可知，参加活动1次、2次和3次的学生人数分别为10、50和40． （I）该合唱团学生参加活动的人均次数为  ．（II）从合唱团中任选两名学生，他们参加活动次数恰好相等的概率为  ．（III）从合唱团中任选两名学生，记“这两人中一人参加1次活动，另一人参加2次活动”为事件 ，“这两人中一人参加2次活动，另一人参加3次活动”为事件 ，“这两人中一人参加1次活动，另一人参加3次活动”为事件．易知  ；  ；的分布列：
的数学期望： ．52、（北京文）（本小题共12分）某条公共汽车线路沿线共有11个车站（包括起点站和终点站），在起点站开出的一辆公共汽车上有6位乘客，假设每位乘客在起点站之外的各个车站下车是等可能的．求： （I）这6位乘客在其不相同的车站下车的概率； （II）这6位乘客中恰有3人在终点站下车的概率； 【解答】（I）这6位乘客在互不相同的车站下车的概率为  ．（II）这6位乘客中恰有3人在终点站下车的概率为  ．53、（安徽理）以  表示标准正态总体在区间（ ）内取值的概率，若随机变量服从正态分布 ，则概率 等于（A）  - （B） （C）  （D） 【解答】以 表示标准正态总体在区间（）内取值的概率，若随机变量服从正态分布，则概率 = = － =，选B。54、（安徽理） (本小题满分13分)在医学生物学试验中，经常以果蝇作为试验对象，一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔.以ξ表示笼内还剩下的果蝇的只数. （Ⅰ）写出ξ的分布列（不要求写出计算过程）； （Ⅱ）求数学期望Eξ； （Ⅲ）求概率P（ξ≥Eξ）. 【解答】本小题主要考查等可能场合下的事件概率的计算、离散型随机变量的分布列、数学期望的概念及其计算，考查分析问题及解决实际问题的能力．本小题满分13分． （Ⅰ） 的分布列为：
（Ⅱ）数学期望为  ．（Ⅲ）所求的概率为  ．55、（安徽文）(本小题满分13分)在医学生物学试验中，经常以果蝇作为试验对象.一个关有6只果蝇的笼子里，不慎混入了两只苍蝇（此时笼内共有8只蝇子：6只果蝇和2只苍蝇），只好把笼子打开一个小孔，让蝇子一只一只地往外飞，直到两只苍蝇都飞出，再关闭小孔. (Ⅰ)求笼内恰好剩下1只果蝇的概率； （Ⅱ）求笼内至少剩下5只果蝇的概率. 【解答】本小题主要考查排列、组合知识与等可能事件、互斥事件概率的计算，运用概率知识分析问题及解决实际问题的能力．本小题满分13分． 以  表示恰剩下 只果蝇的事件 ．以  表示至少剩下 只果蝇的事件 ．可以有多种不同的计算  的方法．方法1（组合模式）：当事件 发生时，第 只飞出的蝇子是苍蝇，且在前 只飞出的蝇子中有1只是苍蝇，所以 ．方法2（排列模式）：当事件 发生时，共飞走只蝇子，其中第只飞出的蝇子是苍蝇，哪一只？有两种不同可能．在前只飞出的蝇子中有 只是果蝇，有 种不同的选择可能，还需考虑这只蝇子的排列顺序．所以 ．由上式立得  ； ．(责任编辑：admin) |
