39、(陕西理 20)设函数f(x)=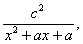 其中a为实数. 其中a为实数.
(Ⅰ)若f(x)的定义域为R,求a的取值范围;
(Ⅱ)当f(x)的定义域为R时,求f(x)的单减区间.
【解答】(Ⅰ) 的定义域为 的定义域为 , , 恒成立, 恒成立,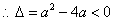 , ,
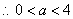 ,即当 ,即当 时 时 的定义域为 的定义域为 . .
(Ⅱ) ,令 ,令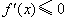 ,得 ,得 . .
由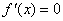 ,得 ,得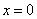 或 或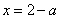 ,又 ,又 , ,
 时,由 时,由 得 得 ; ;
当 时, 时, ;当 ;当 时,由 时,由 得 得 , ,
即当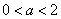 时, 时, 的单调减区间为 的单调减区间为 ; ;
当 时, 时, 的单调减区间为 的单调减区间为 . .
40、(陕西文21)已知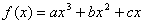 在区间[0,1]上是增函数,在区间 在区间[0,1]上是增函数,在区间 上是减函数,又 上是减函数,又
(Ⅰ)求 的解析式; 的解析式;
(Ⅱ)若在区间 (m>0)上恒有 (m>0)上恒有 ≤x成立,求m的取值范围. ≤x成立,求m的取值范围.
【解答】(Ⅰ)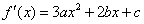 ,由已知 ,由已知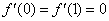 , ,
即 解得 解得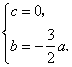
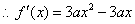 , ,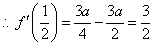 , , , ,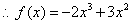 . .
(Ⅱ)令 ,即 ,即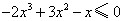 , ,
 , ,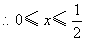 或 或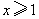 . .
又 在区间 在区间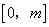 上恒成立, 上恒成立,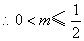 . .
41、(上海理科19)已知函数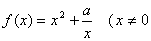 ,常数 ,常数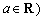 . .
(1)讨论函数 的奇偶性,并说明理由; 的奇偶性,并说明理由;
(2)若函数 在 在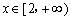 上为增函数,求 上为增函数,求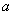 的取值范围. 的取值范围.
【解答】(1)当 时, 时, , ,
对任意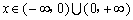 , ,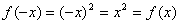 , ,  为偶函数. 为偶函数.
当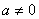 时, 时,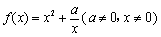 , ,
取 ,得 ,得 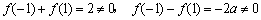 , ,
 , ,
 函数 函数 既不是奇函数,也不是偶函数. 既不是奇函数,也不是偶函数.
(2)解法一:设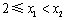 , ,
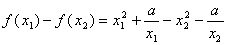  , ,
要使函数 在 在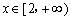 上为增函数,必须 上为增函数,必须 恒成立. 恒成立.
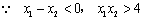 ,即 ,即 恒成立. 恒成立.
又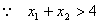 , , . .
 的取值范围是 的取值范围是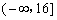 . .
解法二:当 时, 时, ,显然在 ,显然在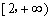 为增函数. 为增函数.
当 时,反比例函数 时,反比例函数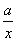 在 在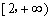 为增函数, 为增函数,
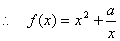 在 在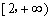 为增函数. 为增函数.
当 时,同解法一. 时,同解法一.
42、(上海文科19)已知函数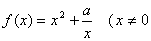 ,常数 ,常数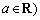 . .
(1)当 时,解不等式 时,解不等式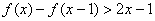 ; ;
(2)讨论函数 的奇偶性,并说明理由. 的奇偶性,并说明理由.
【解答】(1)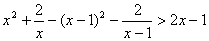 , ,
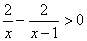 , ,
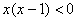 . .
 原不等式的解为 原不等式的解为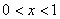 . .
(2)当 时, 时, , ,
对任意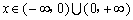 , ,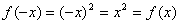 , ,
 为偶函数. 为偶函数.
当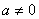 时, 时,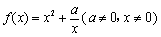 , ,
取 ,得 ,得 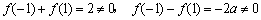 , ,
 , ,
 函数 函数 既不是奇函数,也不是偶函数. 既不是奇函数,也不是偶函数.
43、(四川理 22)设函数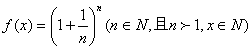 . .
(Ⅰ)当x=6时,求 的展开式中二项式系数最大的项; 的展开式中二项式系数最大的项;
(Ⅱ)对任意的实数x,证明 > >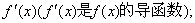
(Ⅲ)是否存在 ,使得an< ,使得an<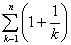 < < 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由. 恒成立?若存在,试证明你的结论并求出a的值;若不存在,请说明理由.
【解答】本题考察函数、不等式、导数、二项式定理、组合数计算公式等内容和数学思想方法。考查综合推理论证与分析解决问题的能力及创新意识。
(Ⅰ)解:展开式中二项式系数最大的项是第4项,这项是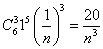
(Ⅱ)证法一:因
  
 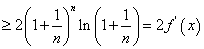
证法二:
因为
  
而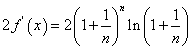
故只需对 和 和 进行比较。 进行比较。
令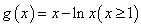 ,有 ,有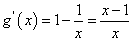
由 ,得 ,得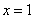
因为当 时, 时, , ,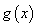 单调递减;当 单调递减;当 时, 时, , ,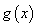 单调递增,所以在 单调递增,所以在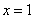 处 处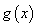 有极小值 有极小值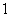
故当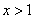 时, 时,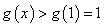 , ,
从而有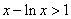 ,亦即 ,亦即
故有 恒成立。 恒成立。
所以 ,原不等式成立。 ,原不等式成立。
(Ⅲ)对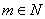 ,且 ,且
有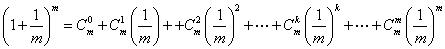
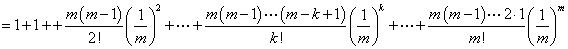 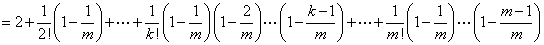


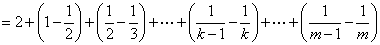
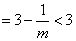
又因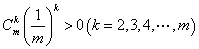 ,故 ,故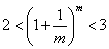
∵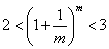 ,从而有 ,从而有 成立, 成立,
即存在 ,使得 ,使得 恒成立。 恒成立。
44、(四川文20)设函数  为奇函数,其图象在点 为奇函数,其图象在点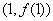 处的切线与直线 处的切线与直线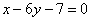 垂直,导函数 垂直,导函数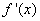 的最小值为 的最小值为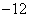 . .
(Ⅰ)求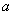 , , , ,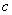 的值; 的值;
(Ⅱ)求函数 的单调递增区间,并求函数 的单调递增区间,并求函数 在 在 上的最大值和最小值. 上的最大值和最小值.
【解答】本题考查函数的奇偶性、单调性、二次函数的最值、导数的应用等基础知识,以及推理能力和运算能力.
(Ⅰ)∵ 为奇函数, 为奇函数,
∴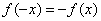
即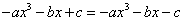
∴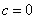
∵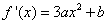 的最小值为 的最小值为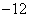
∴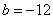
又直线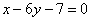 的斜率为 的斜率为
因此,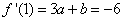
∴ , ,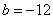 , ,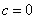 . .
(Ⅱ)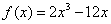 . .
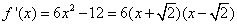 ,列表如下: ,列表如下:
所以函数 的单调增区间是 的单调增区间是 和 和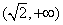
∵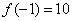 , , , ,
∴ 在 在 上的最大值是 上的最大值是 ,最小值是 ,最小值是 . .
45、(天津理 20)已知函数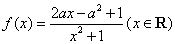 ,其中 ,其中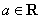 . .
(Ⅰ)当 时,求曲线 时,求曲线 在点 在点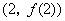 处的切线方程; 处的切线方程;
(Ⅱ)当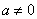 时,求函数 时,求函数 的单调区间与极值. 的单调区间与极值.
【解答】本小题考查导数的几何意义,两个函数的和、差、积、商的导数,利用导数研究函数的单调性和极值等基础知识,考查运算能力及分类讨论的思想方法.满分12分.
(Ⅰ)解:当 时, 时,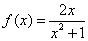 , , , ,
又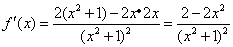 , ,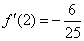 . .
所以,曲线 在点 在点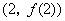 处的切线方程为 处的切线方程为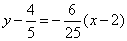 , ,
即 . .
(Ⅱ)解: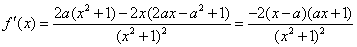 . .
由于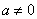 ,以下分两种情况讨论. ,以下分两种情况讨论.
(1)当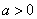 时,令 时,令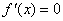 ,得到 ,得到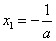 , , .当 .当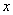 变化时, 变化时, 的变化情况如下表: 的变化情况如下表:
所以 在区间 在区间 , , 内为减函数,在区间 内为减函数,在区间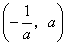 内为增函数. 内为增函数.
函数 在 在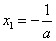 处取得极小值 处取得极小值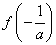 ,且 ,且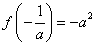 , ,
函数 在 在 处取得极大值 处取得极大值 ,且 ,且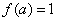 . .
(2)当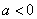 时,令 时,令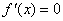 ,得到 ,得到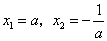 ,当 ,当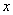 变化时, 变化时, 的变化情况如下表: 的变化情况如下表:
所以 在区间 在区间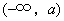 , ,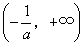 内为增函数,在区间 内为增函数,在区间 内为减函数. 内为减函数.
函数 在 在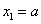 处取得极大值 处取得极大值 ,且 ,且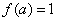 . .
函数 在 在 处取得极小值 处取得极小值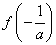 ,且 ,且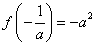 . .
(责任编辑:admin) |