|
30、（湖南理 19）如图4，某地为了开发旅游资源，欲修建一条连接风景点  和居民区 的公路，点所在的山坡面与山脚所在水平面 所成的二面角为 （ ），且 ，点到平面的距离 （km）．沿山脚原有一段笔直的公路 可供利用．从点到山脚修路的造价为 万元/km，原有公路改建费用为 万元/km．当山坡上公路长度为 km（ ）时，其造价为 万元．已知 ， ， ， ．（I）在 上求一点 ，使沿折线 修建公路的总造价最小；（II） 对于（I）中得到的点 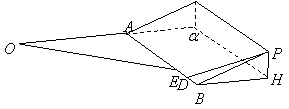，在 上求一点 ，使沿折线 修建公路的总造价最小．（III）在 上是否存在两个不同的点 ， ，使沿折线 修建公路的总造价小于（II）中得到的最小总造价，证明你的结论． 【解答】（I）如图，  ， ，，由三垂线定理逆定理知， ，所以 是山坡与所成二面角的平面角，则 ，  ．设  ， ．则  ．记总造价为  万元，据题设有   当  ，即 时，总造价最小．（II）设  ， ，总造价为 万元，根据题设有  ．则  ，由 ，得 ．当  时， ，在 内是减函数；当  时， ，在 内是增函数．故当 ，即 （km）时总造价最小，且最小总造价为 万元．（III）解法一：不存在这样的点 ，．事实上，在 上任取不同的两点，．为使总造价最小，显然不能位于 与 之间．故可设位于与 之间，且 = ， ， ，总造价为 万元，则 ．类似于（I）、（II）讨论知， ， ，当且仅当 ， 同时成立时，上述两个不等式等号同时成立，此时 ， ，取得最小值，点 分别与点 重合，所以不存在这样的点 ，使沿折线修建公路的总造价小于（II）中得到的最小总造价．解法二：同解法一得    ．当且仅当 且 ，即 同时成立时，取得最小值，以上同解法一．31、（湖南文 21）已知函数  在区间 ， 内各有一个极值点．（I）求  的最大值；（II）当  时，设函数 在点 处的切线为，若在点处穿过函数的图象（即动点在点附近沿曲线运动，经过点时，从的一侧进入另一侧），求函数 的表达式．【解答】（I）因为函数 在区间，内分别有一个极值点，所以  在，内分别有一个实根，设两实根为  （ ），则 ，且 ．于是 ， ，且当  ，即 ， 时等号成立．故的最大值是16．（II）解法一：由  知在点 处的切线的方程是 ，即 ，因为切线 在点 处空过的图象，所以  在 两边附近的函数值异号，则不是 的极值点．而  ，且 ．若  ，则和 都是的极值点．所以  ，即，又由，得 ，故 ．解法二：同解法一得  ．因为切线 在点处穿过的图象，所以在两边附近的函数值异号，于是存在 （ ）．当  时， ，当 时， ；或当 时，，当时，．设  ，则当 时， ，当时，；或当 时， ，当时，．由  知是 的一个极值点，则 ，所以 ，又由，得，故．32、（辽宁理 22）已知函数  ， ．（I）证明：当  时，在 上是增函数；（II）对于给定的闭区间  ，试说明存在实数  ，当 时，在闭区间上是减函数；（III）证明：  ．【解答】本小题主要考察二次函数，利用导数研究函数的单调性和极值，函数的最大值和最小值等知识，考查综合运用数学知识解决问题的能力。 （I）证明：由题设得  ， 。又由 ，且得 ，即 。由此可知，在上是增函数。（II）因为  是为减函数的充分条件，所以只要找到实数k，使得t>k时 ，即 在闭区间上成立即可。因为 在闭区间上连续，故在闭区间上有最大值，设其为k，于是在t>k时，在闭区间上恒成立，即 在闭区间上为减函数。 7分（III）设  ，即 ， 易得  。·········· 9分令  ，则 ，易知 。当 时， ；当 时， 。故当 时， 取最小值， 。所以 ，于是对任意的  ，都有 ，即 。 12分33、（全国一 理20）设函数  ．（Ⅰ）证明： 的导数 ；（Ⅱ）若对所有  都有 ，求的取值范围．【解答】（Ⅰ） 的导数 ．由于  ，故．（当且仅当 时，等号成立）．（Ⅱ）令  ，则 ，（ⅰ）若  ，当时， ，故 在 上为增函数，所以， 时， ，即．（ⅱ）若  ，方程 的正根为 ，此时，若  ，则 ，故在该区间为减函数．所以， 时， ，即 ，与题设相矛盾．综上，满足条件的 的取值范围是 ．(责任编辑：admin) |