1、(北京)已知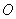 是 是 所在平面内一点, 所在平面内一点,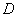 为 为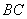 边中点,且 边中点,且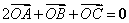 ,那么( A ) ,那么( A )
A. B. B.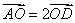
C.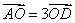 D. D.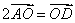
2、(辽宁)若向量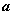 与 与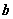 不共线, 不共线,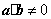 ,且 ,且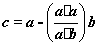 ,则向量 ,则向量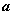 与 与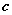 的夹角为( D ) 的夹角为( D )
A.0 B. C. C.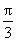 D. D.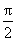
3、(辽宁)若函数 的图象按向量 的图象按向量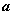 平移后,得到函数 平移后,得到函数 的图象,则向量 的图象,则向量 ( A ) ( A )
A.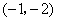 B. B. C. C.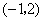 D. D.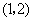
4、(宁夏,海南)已知平面向量 ,则向量 ,则向量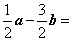 ( D ) ( D )
A.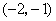 B. B.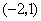
C. D. D.
5、(福建)对于向量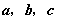 和实数 和实数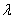 ,下列命题中真命题是( B ) ,下列命题中真命题是( B )
A.若 ,则 ,则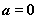 或 或 B.若 B.若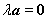 ,则 ,则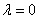 或 或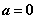
C.若 ,则 ,则 或 或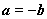 D.若 D.若 ,则 ,则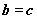
6、(湖北)将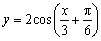 的图象按向量 的图象按向量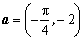 平移,则平移后所得图象的解析式为( A ) 平移,则平移后所得图象的解析式为( A )
A.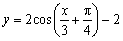 B. B.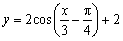
C.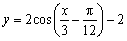 D. D.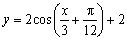
7、(湖北文)设 , ,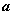 在 在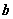 上的投影为 上的投影为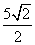 , ,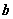 在 在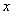 轴上的投影为2,且 轴上的投影为2,且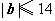 ,则 ,则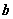 为( B ) 为( B )
A. B. B. C. C.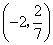 D. D.
8、(湖南)设 是非零向量,若函数 是非零向量,若函数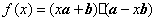 的图象是一条直线,则必有( A ) 的图象是一条直线,则必有( A )
A. B. B. C. C. D. D.
9、(湖南文)若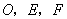 是不共线的任意三点,则以下各式中成立的是( B ) 是不共线的任意三点,则以下各式中成立的是( B )
A.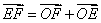 B. B.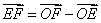
C.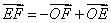 D. D.
10、(四川)设A{a,1},B{2,b},C{4,5},为坐标平面上三点,O为坐标原点,若 上的投影相同,则a与b满足的关系式为 ( A ) 上的投影相同,则a与b满足的关系式为 ( A )
(A)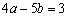 (B) (B)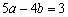 (C) (C)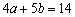 (D) (D)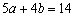
11、(天津)设两个向量 和 和 ,其中 ,其中 为实数.若 为实数.若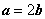 ,则 ,则 的取值范围是( A ) 的取值范围是( A )
A.[-6,1] B. C.(-6,1] D.[-1,6] C.(-6,1] D.[-1,6]
12、(浙江)若非零向量 满足 满足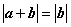 ,则( C ) ,则( C )
A. B. B.
C. D. D. 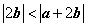
13、(浙江文)若非零向量 、 、 满足| 满足| 一 一 |=| |=| |,则(A) |,则(A)
(A) |2 |>| |>| 一2 一2 | (B) |2 | (B) |2 |<| |<| 一2 一2 | |
(C) |2 |>|2 |>|2 一 一 | (D) |2 | (D) |2 |<|2 |<|2 一 一 | |
14、(山东)在直角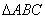 中, 中,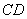 是斜边 是斜边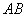 上的高,则下列等式不成立的是( C ) 上的高,则下列等式不成立的是( C )
(A)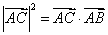 (B) (B) 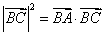
(C)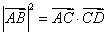 (D) (D) 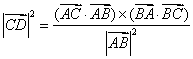
15、(山东文)已知向量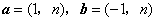 ,若 ,若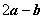 与 与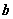 垂直,则 垂直,则 ( C ) ( C )
A. B. B.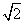 C. C. D.4 D.4
16、(重庆)在 中, 中,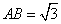 , , , ,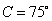 ,则 ,则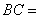 ( A ) ( A )
A. B. B.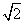 C. C. D. D.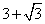
17、(重庆)如题(10)图,在四边形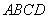 中, 中,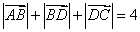 , ,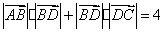 , ,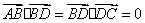 ,则 ,则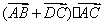 的值为( C ) 的值为( C )
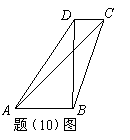 
A. B. B.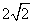 C. C. D. D.
18、(上海)直角坐标系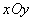 中, 中, 分别是与 分别是与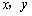 轴正方向同向的单位向量.在直角三角形 轴正方向同向的单位向量.在直角三角形 中,若 中,若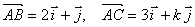 ,则 ,则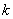 的可能值个数是( B ) 的可能值个数是( B )
A.1 B.2 C.3 D.4
19、(全国Ⅰ)已知向量 , , ,则 ,则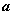 与 与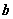 ( A ) ( A )
A.垂直 B.不垂直也不平行 C.平行且同向 D.平行且反向
20、(全国Ⅱ)在 中,已知 中,已知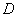 是 是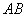 边上一点,若 边上一点,若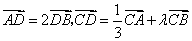 ,则 ,则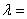 ( A ) ( A )
A. B. B.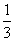 C. C. D. D.
21、(安徽)在四面体 中, 中,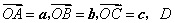 为 为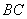 的中点, 的中点, 为 为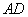 的中点,则 的中点,则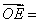  (用 (用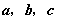 表示) 表示)
22、(北京)已知向量 .若向量 .若向量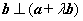 ,则实数 ,则实数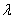 的值是 的值是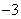
23、(北京)在 中,若 中,若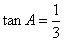 , , , , ,则 ,则 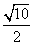
24、(广东)若向量 、 、 满足 满足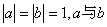 的夹角为120°,则 的夹角为120°,则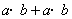 = = 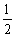 . .
25、(湖南)在 中,角 中,角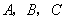 所对的边分别为 所对的边分别为 ,若 ,若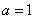 ,b= ,b= , ,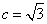 ,则 ,则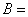 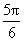 . .
26、(湖南文)在 中,角 中,角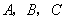 所对的边分别为 所对的边分别为 ,若 ,若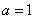 , ,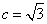 , ,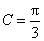 ,则 ,则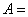  . .
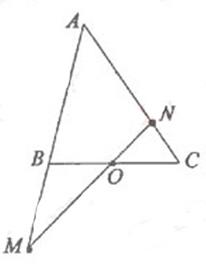
27、(江西理)如图,在 中,点 中,点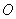 是 是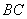 的中点,过点 的中点,过点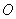 的直线分别交直线 的直线分别交直线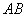 , , 于不同的两点 于不同的两点 ,若 ,若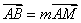 , ,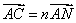 ,则 ,则 的值为 2 . 的值为 2 .
28、(江西文)在平面直角坐标系中,正方形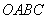 的对角线 的对角线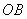 的两端点分别为 的两端点分别为 , ,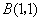 ,则 ,则  . .
29、(陕西)如图,平面内有三个向量 、 、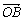 、 、 ,其中与 ,其中与 与 与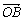 的夹角为120°, 的夹角为120°, 与 与 的夹角为30°,且| 的夹角为30°,且| |=| |=|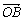 |=1,| |=1,| |= |= ,若 ,若 =λ =λ +μ +μ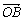 (λ,μ∈R),则λ+μ的值为 (λ,μ∈R),则λ+μ的值为  . .

30、(天津15.)如图,在 中, 中,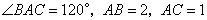 , ,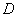 是边 是边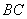 上一点, 上一点,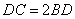 ,则 ,则 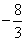 . .
31、(天津文15)在 中, 中,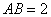 , ,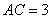 , ,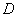 是边 是边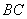 的中点,则 的中点,则 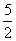 . .
32、(重庆文(13))在△ABC中,AB=1,BC=2,B=60°,则AC= 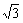 。 。
33、(上海文6.)若向量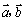 的夹角为 的夹角为 , ,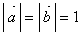 ,则 ,则 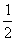 . .
34.(宁夏,海南)17.(本小题满分12分)
如图,测量河对岸的塔高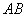 时,可以选与塔底 时,可以选与塔底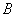 在同一水平面内的两个侧点 在同一水平面内的两个侧点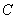 与 与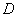 .现测得 .现测得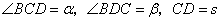 ,并在点 ,并在点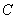 测得塔顶 测得塔顶 的仰角为 的仰角为 ,求塔高 ,求塔高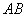 . .
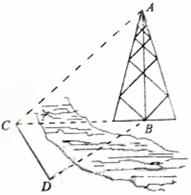
解:在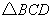 中, 中, . .
由正弦定理得 . .
所以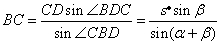 . .
在 中, 中,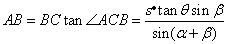 . .
(责任编辑:admin) |