|
一、选择题 1．（全国Ⅰ•理•7题）如图，正四棱柱 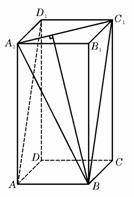 中， ，则异面直线 所成角的余弦值为（ D ） A．  B． C． D． 【解答】如图，连接BC1，A1C1，∠A1BC1是异面直线  与 所成的角，设AB=a，AA1=2a，∴ A1B=C1B= a，A1C1= a，∠A1BC1的余弦值为，选D。2．（全国Ⅱ•理•7题）已知正三棱柱ABC－A1B1C1的侧棱长与底面边长相等，则AB1与侧面ACC1A1所成角的正弦等于（ A ） A．  B． C． D． 【解答】已知正三棱柱ABC－A1B1C1的侧棱长与底面边长相等，取A1C1的中点D1，连接BD1，AD1，∠B1AD1是AB1与侧面ACC1A1所成的角，  ，选A。3．（北京•理•3题）平面  平面 的一个充分条件是（ D ）A．存在一条直线  B．存在一条直线 C．存在两条平行直线  D．存在两条异面直线  【解答】平面 平面的一个充分条件是“存在两条异面直线”，选D。4．（安徽•理•2题）设  ， ， 均为直线，其中，在平面 内，“ ”是 且“ ”的（ ）A．充分不必要条件 B．必要不充分条件 C．充分必要条件 D．既不充分也不必要条件 【解答】设l,m,n均为直线，其中m,n在平面 内，“l ”，则“lm且ln”，反之若“lm且ln”，当m//n时，推不出“l”，∴ “l”是“lm且ln”的充分不必要条件，选A。5．（安徽•理•8题）半径为1的球面上的四点  是正四面体的顶点，则 与 两点间的球面距离为（ ）A．  B． C． D． 【解答】半径为1的球面上的四点 是正四面体的顶点，设AB=a，P为△BCD的中心，O为球心，则OB=1，OP= ，BP= a，由 解得 ，∴ 由余弦定理得∠AOB=arcos(－)，∴ 与两点间的球面距离为，选C。6．（福建•理•8题）已知 ，为两条不同的直线，，为两个不同的平面，则下列命题中正确的是（ D ）A．  B．  C．  D．  【解答】A中m、n少相交条件，不正确；B中分别在两个平行平面的两条直线不一定平行，不正确；C中n可以在 内，不正确，选D 7．（福建•理•10题）顶点在同一球面上的正四棱柱ABCD－A1B1C1D1中，AB＝1，AA1＝  ，则A、C两点间的球面距离为（ B ）A．  B．  C ． D．  【解答】正四棱柱的对角线为球的直径，由4R2=1+1+2=4得R=1，AC=  ，所以∠AOC=（其中O为球心）A、C两点间的球面距离为，选B8．（湖北•理•4题）平面  外有两条直线和，如果和在平面内的射影分别是 和 ，给出下列四个命题：① ⊥ ⊥； ②⊥⊥；③ 与相交与相交或重合； ④与平行与平行或重合；其中不正确的命题个数是（ D ） A.1 B.2 C.3 D.4  【解答】由射影的概念以及线线垂直关系的判定方法，可知①②③④均错, 具体可观察如图的正方体：  但 不垂直，故①错； 但在底面上的射影都是 故②错；  相交，但 异面，故③错； 但 异面，故④错点评：本题主要考察空间线面之间位置关系，以及射影的意义理解。关键是要理解同一条直线在不同平面上的射影不同；线在面内，线面平行，线面相交的不同位置下，射影也不相同。要从不用的方向看三垂线定理，充分发挥空间想象力。 易错点：空间想象力不够，容易误判③、④正确，而错选B或C 9．（湖南•理•8题）棱长为1的正方体  的8个顶点都在球 的表面上， 分别是棱 ， 的中点，则直线 被球截得的线段长为（ D ）A． B． C． D． 【解答】正方体对角线为球直径，所以  ，在过点E、F、O的球的大圆中，由已知得d= ， ，所以EF=2r=。10．（江苏•理•4题）已知两条直线  ，两个平面 ，给出下面四个命题：①  ②③  ④ 其中正确命题的序号是（ C ） A．①③ B．②④ C．①④ D．②③ 【解答】用线面垂直的性质和面面平行的性质可判断①④ 正确，②中m,n可以平行或异面③中n可以在 内 选C11．如图，正方体  的棱长为，过点作平面 的垂线，垂足为点 ，则以下命题中，错误的命题是（ ）A．点 是 的垂心 B． 垂直平面 C． 的延长线经过点 D．直线和 所成角为  【解答】因为三棱锥A— 是正三棱锥，故顶点A在底面的射映是底面中心，A正确；面∥面，而AH垂直平面，所以AH垂直平面，B正确；根据对称性知C正确。选D12．（辽宁•理•7题）若  是两条不同的直线， 是三个不同的平面，则下列命题中的真命题是（ ）A．若  ，则 B．若  ， ，则 C．若  ， ，则 D．若 ， ，则 【解答】由有关性质排除A、B、D，选C 13．（陕西•理•6题）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ B ） A．  B． C．  D． 【解答】正三棱锥的高为1，由平面几何知识知底面边长为  ，体积为 ，选C14．（四川•理•4题）如图， 为正方体，下面结论错误的是（ ） （A）  平面 （B） （C）  平面 （D）异面直线 与 所成的角为 【解答】选D．显然异面直线 与所成的角为 15．(宁夏•理•8题) 已知某个几何体的三视图如下，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ B ）   A．  B． C． D． 【解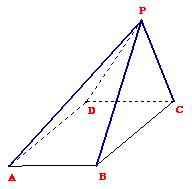答】如图，   16．（四川•理•6题）设球O的半径是1，A、B、C是球面上三点，已知A到B、C两点的球面距离都是  ，且三面角B-OA-C的大小为 ，则从A点沿球面经B、C两点再回到A点的最短距离是（ C ） A．  B． C． D． 【解答】选C．  ．本题考查球面距离．17．（天津•理•6题）设  为两条直线， 为两个平面，下列四个命题中，正确的命题是（ D ）A．若 与所成的角相等，则 B．若 ，，则C．若  ，则 D．若 ，，则 【解答】对于A当  与 均成 时就不一定；对于B只需找个  ，且 即可满足题设但不一定平行；对于C可参考直三棱柱模型排除，故选D18．（浙江•理•6题）若P是两条异面直线  外的任意一点，则（ B ）A．过点P有且仅有一条直线与 都平行 B．过点P有且仅有一条直线与都垂直C．过点P有且仅有一条直线与 都相交 D．过点P有且仅有一条直线与都异面【解答】设过点P的直线为 ，若与l、m都平行，则l、m平行，与已知矛盾，故选项A错误。由于l、m只有惟一的公垂线，而过点P与公垂线平行的直线只有一条，故B正确。对于选项C、D可参考右图的正方体，设AD为直线l， 为直线m;若点P在P1点，则显然无法作出直线与两直线都相交，故选项C错误。若P在 点，则由图中可知直线 均与l、m异面，故选项D错误。 (责任编辑：admin) |