17、(07安徽)定义在R上的函数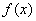 既是奇函数,又是周期函数, 既是奇函数,又是周期函数, 是它的一个正周期.若将方程 是它的一个正周期.若将方程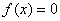 在闭区间 在闭区间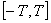 上的根的个数记为 上的根的个数记为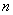 ,则 ,则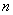 可能为 可能为
A.0 B.1 C.3 D.5
答案:D.
18、(07安徽)图中的图象所表示的函数的解析式为
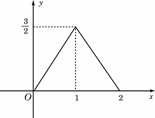
(A)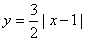 (0≤x≤2) (B) (0≤x≤2) (B) 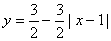 (0≤x≤2) (0≤x≤2)
(C) 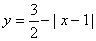 (0≤x≤2) (D) (0≤x≤2) (D) 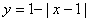 (0≤x≤2) (0≤x≤2)
答案:B.
19、(07安徽)设a>1,且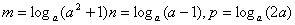 ,则 ,则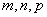 的大小关系为 的大小关系为
(A) n>m>p (B) m>p>n (C) m>n>p (D) p>m>n
答案:B.
20、(07北京)对于函数①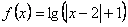 ,② ,②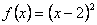 ,③ ,③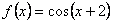 .判断如下三个命题的真假:命题甲: .判断如下三个命题的真假:命题甲: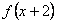 是偶函数;命题乙: 是偶函数;命题乙: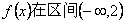 上是减函数,在区间 上是减函数,在区间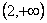 上是增函数;命题丙: 上是增函数;命题丙: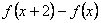 在 在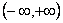 上是增函数.能使命题甲、乙、丙均为真的所有函数的序号是() 上是增函数.能使命题甲、乙、丙均为真的所有函数的序号是()
A.①③ B.①② C. ③ D. ②
答案:D
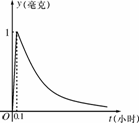
21、(07湖北)为了预防流感,某学校对教室用药熏消毒法进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为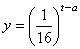 (a为常数),如图所示,根据图中提供的信息,回答下列问题: (a为常数),如图所示,根据图中提供的信息,回答下列问题:
(Ⅰ)从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为 .
(Ⅱ)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过 小时后,学生才能回到教室.
答案: 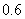
22、(07山东)函数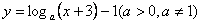 的图象恒过定点A,若点A在直线 的图象恒过定点A,若点A在直线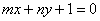 上,其中 上,其中 ,则 ,则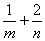 的最小值为 . 的最小值为 .
答案:8
23、(07重庆)若函数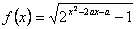 的定义域为R,则实数 的定义域为R,则实数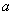 的取值范围 。 的取值范围 。
答案: 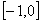
24、(07宁夏)设函数 为奇函数,则实数 为奇函数,则实数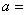 。 。
答案:-1
25、(07全国Ⅰ)函数 的图象与函数 的图象与函数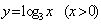 的图象关于直线 的图象关于直线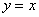 对称,则 对称,则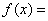 __________。 __________。
答案: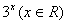
26、(07北京)已知函数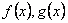 分别由下表给出: 分别由下表给出:
则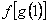 的值 ;满足 的值 ;满足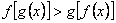 的 的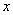 的值 . 的值 .
答案:1,2
27、(07广东)已知a是实数,函数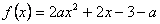 ,如果函数 ,如果函数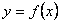 在区间 在区间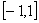 上有零点,求a的取值范围. 上有零点,求a的取值范围.
解:若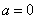 , , 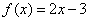 ,显然在 ,显然在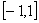 上没有零点, 所以 上没有零点, 所以 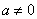 . .
令 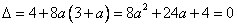 , 解得 , 解得 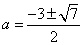
①当 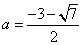 时, 时, 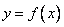 恰有一个零点在 恰有一个零点在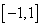 上; 上;
②当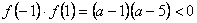 ,即 ,即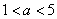 时, 时,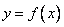 在 在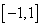 上也恰有一个零点. 上也恰有一个零点.
③当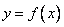 在 在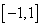 上有两个零点时, 则 上有两个零点时, 则
 或 或
解得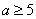 或 或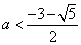
综上所求实数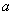 的取值范围是 的取值范围是 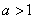 或 或 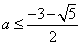 . .
28、(07北京)已知集合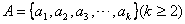 其中 其中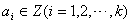 ,由 ,由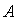 中的元素构成两个相应的集合 中的元素构成两个相应的集合 , , ,其中 ,其中 是有序实数对,集合 是有序实数对,集合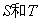 的元素个数分别为 的元素个数分别为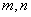 . .
若对于任意的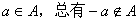 ,则称集合 ,则称集合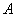 具有性质 具有性质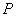 . .
(Ⅰ)检验集合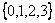 与 与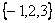 是否具有性质 是否具有性质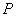 ,并对其中具有性质 ,并对其中具有性质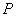 的集合写出相应的集合 的集合写出相应的集合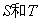 ; ;
(Ⅱ)对任何具有性质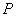 的集合 的集合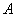 ,证明: ,证明: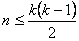 ; ;
(Ⅲ)判断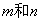 的大小关系,并证明你的结论. 的大小关系,并证明你的结论.
(Ⅰ)解:集合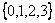 不具有性质 不具有性质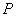 , ,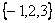 具有性质 具有性质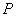 ,其相应的集合 ,其相应的集合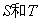 是 是
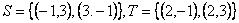 ; ;
(Ⅱ)证明:首先由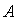 中的元素构成的有序实数对共有 中的元素构成的有序实数对共有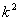 个,因为 个,因为
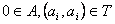 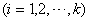 , ,
又因为当 , ,
所以当 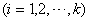 ,于是集合 ,于是集合 中的元素的个数最多为 中的元素的个数最多为
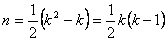 ,即 ,即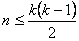 . .
(Ⅲ)解: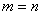 ,证明如下: ,证明如下:
①对于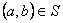 ,根据定义 ,根据定义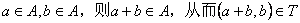
如果 是 是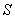 中的不同元素,那么 中的不同元素,那么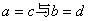 中至少有一个不成立,于是 中至少有一个不成立,于是 与 与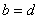 中至少有一个不成立,故 中至少有一个不成立,故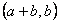 与 与 也是 也是 中的不同元素.可见 中的不同元素.可见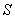 中的元素个数不多于 中的元素个数不多于 中的元素个数,即 中的元素个数,即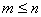 ; ;
②对于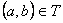 ,根据定义 ,根据定义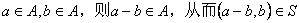 如果 如果 是 是 中的不同元素,那么 中的不同元素,那么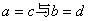 中至少有一个不成立,于是 中至少有一个不成立,于是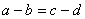 与 与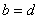 中至少有一个不成立,故 中至少有一个不成立,故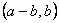 与 与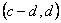 也是 也是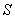 中的不同元素.可见 中的不同元素.可见 中的元素个数不多于 中的元素个数不多于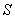 中的元素个数,即 中的元素个数,即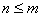 . .
由①②可知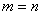 . .
(责任编辑:admin) |