|
四川省遂宁市第一中学校 唐振钧 线性规划问题,明确线性目标函数Z=mx+ny(m≠0,n≠0)中Z的几何意义是线性规划问题的核心、是解决线性规划问题的关键.由Z=mx+ny得,y= 1.当n>0时,z=nb, z与y= 例1 (2006高考天津)设变量  ,则目标函数 ,则目标函数A. 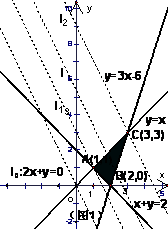 分析:y=-2x+z与y=-2x+b比较,z=b, b越大,z越大;b越小,z越小. 解:作出不等式组  所表示的平面区域(图1),即可行域△ABC. 所表示的平面区域(图1),即可行域△ABC. 解 作直线l0:2x+y=0,作与l0平行的直线l,则当l经过可行域上的点A时(直线l1),目标函数 例2(2006高考广东)在约束条件 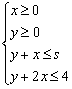 下,当 下,当A. 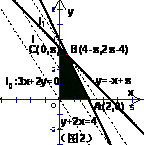  分析:s变化,可行域也将发生变化. 解:由 (1)当 可行域是四边形OABC,此时,zmax=3(4-s)+2(2s-4)=s+4, ∵3≤s<4,∴7≤s+4<8,故7≤zmax<8. (2)当 可行域是△OAE,此时,zmax=3×0+2×4=8. ∴综上得,7≤zmax≤8.故选D. 2.当n<0时,z=nb, z与y= 例3(2006高考安徽)如果实数 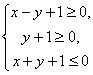 那么 那么A.  分析:y=2x-z与y=2x+b比较,z= -b, b越大,z越大;b越小,z越小. 解:作出不等式组 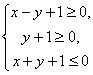 所表示的平面区域(图5),即可行域△ABC. 所表示的平面区域(图5),即可行域△ABC.解 作直线l0:2x-y=0,作与l0平行的直线l,当直线l过可行域上的点C时(直线l1),目标函数z=2x-y取最大值,zmax=2×0-(-1)=1.故选B. 例4 (2006高考重庆)已知变量 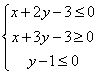 .若目标函数 .若目标函数分析:可行域是一个有界区域(△ABC),若线性目标函数有最大值或最小值,则应在边界点取得最大值或最小值. 解:作出不等式组 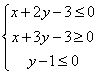 表示的平面区域(图6),即可行域△ABC. 表示的平面区域(图6),即可行域△ABC. 解 ∵目标函数 ∴ 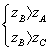 即 即(责任编辑:admin) |
