|
51、(湖北理)(本小题满分12分)在平面直角坐标系 (I)若点 (II)是否存在垂直于  【解答】本小题主要考查直线、圆和抛物线等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力. 解法1:(Ⅰ)依题意,点 直线 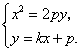 消去 消去 由韦达定理得 于是 (Ⅱ)假设满足条件的直线  令 即抛物线的通径所在的直线. 解法2:(Ⅰ)前同解法1,再由弦长公式得 又由点到直线的距离公式得 从而 (Ⅱ)假设满足条件的直线 将直线方程 则 设直线 则有 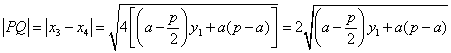 . .令 即抛物线的通径所在的直线. 52、(湖北文)过双曲线 【解答】根据双曲线定义有|MF2|-|MF|=2a,|NF2|-|NF|=2a,两式相加得|MF2|+|NF2|-|MN|=4a=8 点评:本题主要考查双曲线定义的灵活运用。 53、(广东理)在平面直角坐标系 【解答】OA的垂直平分线的方程是y- 54、(广东理)(本小题满分14分)在平面直角坐标系 (1)求圆 (2)试探究圆 【解答】(1)设圆心坐标为(m,n)(m<0,n>0),则该圆的方程为(x-m)2+(y-n)2=8已知该圆与直线y=x相切,那么圆心到该直线的距离等于圆的半径,则 即 又圆与直线切于原点,将点(0,0)代入得 m2+n2=8 ② 联立方程①和②组成方程组解得 故圆的方程为(x+2)2+(y-2)2=8 (2) 其焦距c= 要探求是否存在异于原点的点Q,使得该点到右焦点F的距离等于 通过联立两圆的方程解得x= 即存在异于原点的点Q( 55、(广东文)在平面直角坐标系 【解答】设所求抛物线方程为 56、(广东文)(本小题满分14分)在平面直角坐标系 (1)求圆 (2)试探究圆 【解答】设圆C 的圆心为 (m, n) 则  解得 解得所求的圆的方程为 (2) 由已知可得 椭圆的方程为 假设存在Q点 整理得 因此不存在符合题意的Q点. 57、(福建理)以双曲线 A. C. 【解答】右焦点即圆心为(5,0),一渐近线方程为 58、(福建理)(本小题满分12分)如图,已知点   (Ⅰ)求动点 (Ⅱ)过点 【解答】本小题主要考查直线、抛物线、向量等基础知识,考查轨迹方程的求法以及研究曲线几何特征的基本方法,考查运算能力和综合解题能力.满分14分. 解法一:(Ⅰ)设点   (Ⅱ)设直线 设 联立方程组  ,消去 ,消去 由 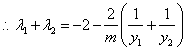 解法二:(Ⅰ)由 所以点 (Ⅱ)由已知 则:  .…………① .…………①过点 则有:  .…………② .…………②由①②得: 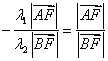 ,即 ,即(责任编辑:admin) |
