|
33、（浙江文）已知数列{  }中的相邻两项 、 是关于x的方程 的两个根，且≤ (k ＝1，2，3，…)．(I)求  及 (n≥4)(不必证明)；(Ⅱ)求数列{ }的前2n项和S2n．本题主要考查等差、等比数列的基本知识，考查运算及推理能力．满分14分． (I)解：方程 的两个根为 ．当k＝1时，  ，所以 ；当k＝2时，  ，所以 ；当k＝3时，  ，所以 ；当k＝4时，  ，所以 ；因为n≥4时，  ，所以 （Ⅱ）  ＝ ．34、（天津理）在数列  中， ，其中 ．（Ⅰ）求数列 的通项公式；（Ⅱ）求数列 的前 项和 ；（Ⅲ）证明存在  ，使得 对任意 均成立．本小题以数列的递推关系式为载体，主要考查等比数列的前 项和公式、数列求和、不等式的证明等基础知识与基本方法，考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力．满分14分．（Ⅰ）解法一：  ， ， ．由此可猜想出数列 的通项公式为 ．以下用数学归纳法证明． （1）当  时，，等式成立．（2）假设当  时等式成立，即 ，那么    ．这就是说，当  时等式也成立．根据（1）和（2）可知，等式对任何都成立．解法二：由  ，，可得  ，所以  为等差数列，其公差为1，首项为0，故 ，所以数列的通项公式为．（Ⅱ）解：设  ， ① ②当  时，①式减去②式，得  ， ．这时数列 的前项和 ．当  时， ．这时数列的前项和 ．（Ⅲ）证明：通过分析，推测数列  的第一项 最大，下面证明： ． ③由 知 ，要使③式成立，只要 ，因为    ．所以③式成立． 因此，存在  ，使得 对任意均成立．35、（天津文）在数列 中，， ， ．（Ⅰ）证明数列  是等比数列；（Ⅱ）求数列 的前项和；（Ⅲ）证明不等式  ，对任意皆成立．本小题以数列的递推关系式为载体，主要考查等比数列的概念、等比数列的通项公式及前 项和公式、不等式的证明等基础知识，考查运算能力和推理论证能力．满分12分．（Ⅰ）证明：由题设 ，得 ，．又  ，所以数列是首项为 ，且公比为 的等比数列．（Ⅱ）解：由（Ⅰ）可知  ，于是数列的通项公式为 ．所以数列 的前项和 ．（Ⅲ）证明：对任意的 ，  ．所以不等式 ，对任意皆成立．36、（四川文）已知函数f（x）=x2－4，设曲线y＝f（x）在点（xn，f（xn））处的切线与x轴的交点为（xn+1,u）（u,N +），其中为正实数. （Ⅰ）用xx表示xn+1； （Ⅱ）若a1=4，记an=lg  ，证明数列｛a1｝成等比数列，并求数列｛xn｝的通项公式；（Ⅲ）若x1＝4，bn＝xn－2，Tn是数列｛bn｝的前n项和，证明Tn<3. 解析：本题综合考查数列、函数、不等式、导数应用等知识，以及推理论证、计算及解决问题的能力． （Ⅰ）由题可得  ．所以曲线  在点 处的切线方程是： ．即  ．令  ，得 ．即  ．显然  ，∴ ．（Ⅱ）由 ，知 ，同理 ．故  ．从而  ，即 ．所以，数列 成等比数列．故  ．即  ．从而  所以  （Ⅲ）由（Ⅱ）知 ，∴  ∴  当 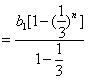时，显然 ．当  时， ∴     ．综上，   ． 37、（上海理）若有穷数列  （是正整数），满足 即 （ 是正整数，且 ），就称该数列为“对称数列”。（1）已知数列  是项数为7的对称数列，且 成等差数列， ，试写出的每一项（2）已知  是项数为 的对称数列，且 构成首项为50，公差为 的等差数列，数列的前 项和为 ，则当 为何值时，取到最大值？最大值为多少？（3）对于给定的正整数  ，试写出所有项数不超过 的对称数列，使得 成为数列中的连续项；当 时，试求其中一个数列的前2008项和 解：（1）设  的公差为 ，则 ，解得  ， 数列为 ． （2）   ，  ，当 时， 取得最大值． 的最大值为626． （3）所有可能的“对称数列”是： ①  ；②  ；③  ；④  ． 对于①，当  时， ． 当  时，   ． 对于②，当 时， ． 当 时，  ．对于③，当 时， ． 当 时， ．对于④，当 时，． 当 时， ．38、（上海文）如果有穷数列  （ 为正整数）满足条件 ， ，…， ，即 （ ），我们称其为“对称数列”． 例如，数列  与数列 都是“对称数列”． （1）设 是7项的“对称数列”，其中 是等差数列，且 ， ．依次写出的每一项；（2）设  是 项的“对称数列”，其中 是首项为，公比为 的等比数列，求各项的和 ；（3）设  是 项的“对称数列”，其中 是首项为，公差为 的等差数列．求 前项的和  ． 解：（1）设数列 的公差为，则，解得 ，数列为． （2）      67108861． （3）  ． 由题意得  是首项为 ，公差为 的等差数列． 当  时，  ． 当  时，   ．综上所述，  (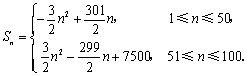责任编辑：admin) |