|
1、（重庆文）已知以F1（2,0），F2（2,0）为焦点的椭圆与直线  有且仅有一个交点，则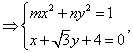椭圆的长轴长为（ C ）（A）  （B） （C） （D） 【解答】设椭圆方程为   消x得： 即： 又 联立解得 由焦点在x轴上，故长轴长为 2、（重庆文）（21）（本小题满分12分，（Ⅰ）小问4分，（Ⅱ）小问8分） 如题（21）图，倾斜角为a的直线经过抛物线  的焦点F，且与抛物线交于A、B两点。 题（21）图 （Ⅰ）求抛物线的焦点F的坐标及准线l的方程； （Ⅱ）若a为锐角，作线段AB的垂直平分线m交x轴于点P，证明|FP|-|FP|cos2a为定值，并求此定值。 【解答】（Ⅰ）设抛物线的标准方程为  ，则 ，从而 因此焦点  的坐标为（2，0）.又准线方程的一般式为  。从而所求准线l的方程为 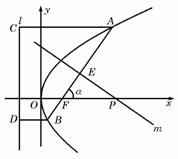 。 答（21）图 （Ⅱ）解法一：如图（21）图作AC⊥l，BD⊥l，垂足为C、D，则由抛物线的定义知 |FA|=|FC|,|FB|=|BD|. 记A、B的横坐标分别为xxxz，则 |FA|＝|AC|＝  解得 ，类似地有  ，解得 。记直线m与AB的交点为E，则  所以 。故  。解法二：设  ， ，直线AB的斜率为 ，则直线方程为 。将此式代入 ,得 ，故 。记直线m与AB的交点为  ，则 ， ，故直线m的方程为  .令y=0,得P的横坐标  故 。从而 为定值。3、（重庆理）过双曲线  的右焦点F作倾斜角为 的直线，交双曲线于PQ两点，则|FP||FQ|的值为__________. 【分析】：    代入 得： 设  又   4、（重庆理）(本小题满分12分)如图，中心在原点O的椭圆的右焦点为F（3，0），右准线l的方程为：x = 12。 （1）求椭圆的方程； （2）在椭圆上任取三个不同点  ，使 ，证明 为定值，并求此定值。
 解：（I）设椭圆方程为  ．因焦点为 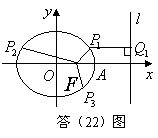 ，故半焦距 ．  又右准线  的方程为 ，从而由已知 ，因此  ， ．故所求椭圆方程为  ．（II）记椭圆的右顶点为  ，并设 （ 1，2，3），不失一般性，假设  ，且 ， ．又设点  在上的射影为 ，因椭圆的离心率 ，从而有   ．解得  ．因此  ，而   ，故  为定值．5、（浙江文）已知双曲线   的左、右焦点分别为F1、F2，P是准线上一点，且P F1⊥P F2，｜P F1｜ ｜P F2 ｜＝4ab，则双曲线的离心率是（B）(A)  (B)  (C)2 (D)3【解答】：设准线与x轴交于A点. 在  中,   , 又  ,化简得  , 故选答案B【高考考点】双曲线的离心率的求法解三角形的相关知识。 【易错点】：不能联系三角形的有关知识，找不到解题方法而乱选。 【备考提示】：双曲线的离心率的求法是解析几何的一个重点，且方法较多，要善于总结各种方法，灵活应用。 6、（浙江文）(本题15分)如图，直线y＝kx＋b与椭圆  交于A、B两点，记△AOB的面积为S．（I）求在k＝0，0＜b＜1的条件下，S的最大值； （Ⅱ）当｜AB｜＝2，S＝1时，求直线AB的方程．  本题主要考查椭圆的几何性质、椭圆与直线的位置关系等基础知识，考查解析几何的基本思想方法和综合解题能力． （Ⅰ）解：设点 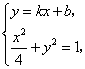的坐标为 ，点 的坐标为 ，由 ，解得 ，所以    ．当且仅当  时， 取到最大值 ．（Ⅱ）解：由  得 ， ，①  ． ②设  到 的距离为 ，则 ，又因为  ，所以 ，代入②式并整理，得 ，解得 ， ，代入①式检验， ，故直线 的方程是 或 或 ，或 ．【高考考点】椭圆的几何性质、椭圆与直线的位置关系等知识 【易错点】：不能准确计算或轻易舍掉一些答案。 【备考提示】：本题主要考查椭圆的几何性质、椭圆与直线的位置关系等基础知识，考查解析几何的基本思想方法和综合解题能力．故此类问题一方面要求考生能熟练掌握相关知识，并且能够有较高的分析问题和解决问题的能力，同时还要有较强的运算能力和不懈的毅力。 7、（浙江理）已知双曲线  的左、右焦点分别为 ， ， 是准线上一点，且 ， ，则双曲线的离心率是（ B ）A． B． C． D． 【分析】：设准线与x轴交于A点. 在 中, , 又 ,化简得 , 故选答案B8、（天津文）设双曲线  的离心率为，且它的一条准线与抛物线 的准线重合，则此双曲线的方程为（ D ）A．  B． C．  D． 【解析】∵抛物线 的准线为 ,故有 ------①又∵双曲线 的离心率为,故有: -------②, ①  ②得到 ,进而求出 , ∴双曲线的方程为(责任编辑：admin) |
