|
62、(北京文)椭圆 A. 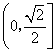 C. C. 【解答】椭圆  ,选D。 ,选D。63、(北京文)如图,矩形 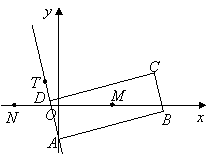 (I)求 (II)求矩形 (III)若动圆 【解答】(I)因为 又因为点 所以 (II)由 因为矩形 所以 又 从而矩形 (III)因为动圆 所以 即 故点 因为实半轴长 所以虚半轴长 从而动圆 64、(安徽理)如图, 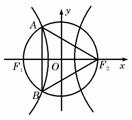 (A) 【解答】如图, 65、(安徽理)如图,抛物线y=-x2+1与x轴的正半轴交于点A,将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线,与抛物线的交点依次为Q1,Q2,…,Qn-1,从而得到n-1个直角三角形△Q1OP1, △Q2P1P2,…, △Qn-1Pn-1Pn-1,当n→∞时,这些三角形的面积之和的极限为 .  【解答】如图,抛物线y=-x2+1与x轴的正半轴交于点A(1,0),将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线,与抛物线的交点依次为Q1,Q2,…,Qn-1,从而得到n-1个直角三角形△Q1OP1, △Q2P1P2,…, △Qn-1Pn-2Pn-1, ∴ 整理得 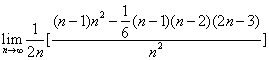 = =66、(安徽理)如图,曲线G的方程为y2=2x(y≥0).以原点为圆心,以t(t >0)为半径的圆分别与曲线G和y轴的正半轴相交于点A与点B.直线AB与x轴相交于点C. 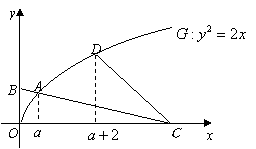 (Ⅰ)求点A的横坐标a与点C的横坐标c的关系式; (Ⅱ)设曲线G上点D的横坐标为a+2,求证:直线CD的斜率为定值. 【解答】本小题综合考查平面解析几何知识,主要涉及平面直角坐标系中的两点间距离公式、直线的方程与斜率、抛物线上的点与曲线方程的关系,考查运算能力与思维能力、综合分析问题的能力.本小题满分12分. 解:(Ⅰ)由题意知, 因为 由于 由点 直线 又因点 将(1)代入上式,得 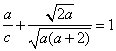 , ,解得 (Ⅱ)因为 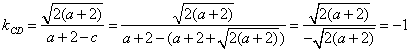 . .所以直线 67、(安徽文)椭圆 (A) 【解答】椭圆 68、(安徽文)设F是抛物线G:x2=4y的焦点. (Ⅰ)过点P(0,-4)作抛物线G的切线,求切线方程: (Ⅱ)设A、B为势物线G上异于原点的两点,且满足 【解答】本小题主要考查抛物线的方程与性质,抛物线的切点与焦点,向量的数量积,直线与抛物线的位置关系,平均不等式等基础知识,考查综合分析问题、解决问题的能力. 解:(I)设切点 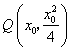 .由 .由即 因为点 所以 所求切线方程为 (II)设 由题意知,直线 因直线 点 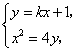 得 由根与系数的关系知  因为 同理可求得  . .当 (责任编辑:admin) |
