一、填空题(本题满分60分,前4题每小题7分,后4小题每小题8分)
1. 方程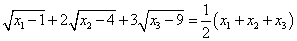 的实数解 的实数解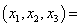 _______________. _______________.
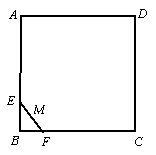
2. 有一条长度为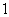 的线段 的线段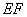 ,其端点 ,其端点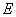 , ,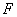 在边长为 在边长为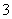 的正方形 的正方形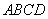 的四边上滑动,当 的四边上滑动,当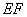 绕着正方形的四边滑动一周时, 绕着正方形的四边滑动一周时,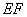 的中点 的中点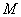 所形成的轨迹的长是_______________. 所形成的轨迹的长是_______________.
3. 复数数列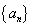 满足 满足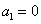 , ,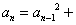 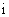 ( (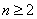 , ,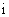 为虚数单位),则它的前 为虚数单位),则它的前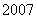 项的和为_______________. 项的和为_______________.
4. 已知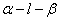 是大小为 是大小为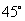 的二面角, 的二面角,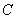 为二面角内一定点,且到半平面 为二面角内一定点,且到半平面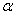 和 和 的距离分别为 的距离分别为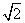 和 和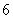 , ,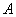 , ,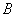 分别是半平面 分别是半平面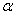 , , 内的动点,则 内的动点,则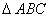 周长的最小值为_______________. 周长的最小值为_______________.
5. 已知平面直角坐标系中点与点的对应法则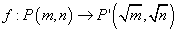 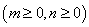 .若一段曲线在对应法则 .若一段曲线在对应法则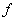 下对应椭圆的一段弧 下对应椭圆的一段弧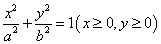 ,则这段曲线的方程是________________. ,则这段曲线的方程是________________.
6. 已知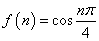 ,计算: ,计算: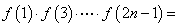 _______________. _______________.
7. 已知数列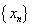 满足 满足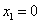 , ,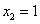 , ,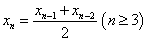 ,则数列 ,则数列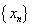 的通项公式 的通项公式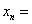 _______________. _______________.
8. 已知圆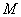 : :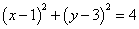 ,过 ,过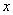 轴上的点 轴上的点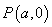 存在圆 存在圆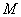 的割线 的割线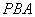 ,使得 ,使得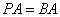 ,则点 ,则点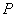 的横坐标 的横坐标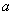 的取值范围是_______________. 的取值范围是_______________.
二、解答题
9.(本题满分14分)对任意正整数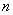 ,用 ,用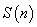 表示满足不定方程 表示满足不定方程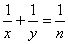 的正整数对 的正整数对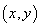 的个数,例如,满足 的个数,例如,满足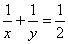 的正整数对有 的正整数对有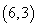 , ,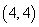 , ,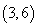 三个,则 三个,则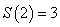 .求出使得 .求出使得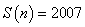 的所有正整数 的所有正整数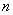 . .
10. (本题满分14分)已知关于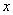 的方程 的方程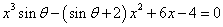 有三个正实根,求 有三个正实根,求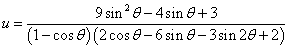 的最小值. 的最小值.
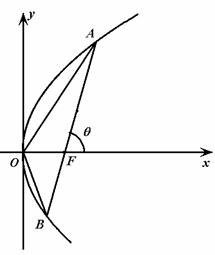
11. (本题满分16分)已知抛物线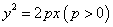 , ,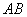 是过焦点 是过焦点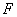 的弦,如果 的弦,如果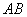 与 与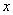 轴所成的角为 轴所成的角为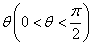 ,求 ,求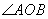 . .
12. (本题满分16分)求满足如下条件的最小正整数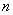 ,在圆周上任取 ,在圆周上任取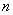 个点 个点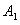 , ,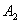 ,…, ,…,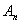 ,则在 ,则在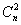 个角 个角 中,至少有 中,至少有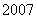 个不超过 个不超过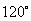 . .
2007年上海市高中数学竞赛试卷参考答案
1. (2,8,18) 2. 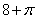 3. –1003+2 i 4. 3. –1003+2 i 4. 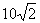
5. 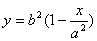 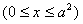 6. 6. 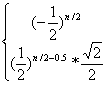 
7. 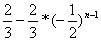 8 8 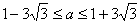
9. 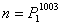 或者 或者 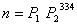 或者 或者 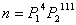 或者 或者 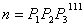

10 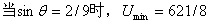
11. 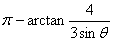
12 91
(责任编辑:admin) |