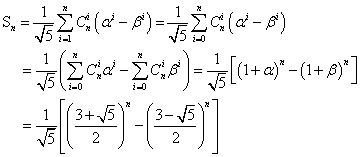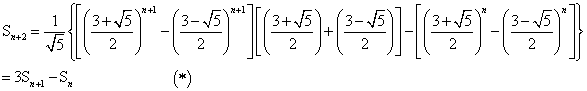基础知识
整数的性质有很多,这里我们着重讨论整数的整除性、整数的奇偶性,质数与合数、完全平方数及整数的尾数等几个方面的应用。
1.整除的概念及其性质
在高中数学竞赛中如果不加特殊说明,我们所涉及的数都是整数,所采用的字母也表示整数。
定义:设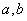 是给定的数, 是给定的数,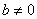 ,若存在整数 ,若存在整数 ,使得 ,使得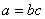 则称 则称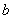 整除 整除 ,记作 ,记作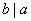 ,并称 ,并称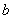 是 是 的一个约数(因子),称 的一个约数(因子),称 是 是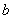 的一个倍数,如果不存在上述 的一个倍数,如果不存在上述 ,则称 ,则称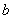 不能整除 不能整除 记作 记作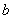 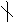  。 。
由整除的定义,容易推出以下性质:
(1)若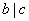 且 且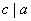 ,则 ,则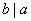 (传递性质); (传递性质);
(2)若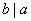 且 且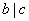 ,则 ,则 即为某一整数倍数的整数之集关于加、减运算封闭。若反复运用这一性质,易知 即为某一整数倍数的整数之集关于加、减运算封闭。若反复运用这一性质,易知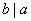 及 及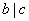 ,则对于任意的整数 ,则对于任意的整数 有 有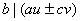 。更一般,若 。更一般,若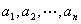 都是 都是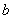 的倍数,则 的倍数,则 。或着 。或着 ,则 ,则 其中 其中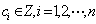 ; ;
(3)若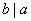 ,则或者 ,则或者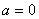 ,或者 ,或者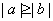 ,因此若 ,因此若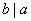 且 且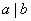 ,则 ,则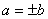 ; ;
(4)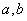 互质,若 互质,若 ,则 ,则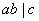 ; ;
(5) 是质数,若 是质数,若 ,则 ,则 能整除 能整除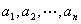 中的某一个;特别地,若 中的某一个;特别地,若 是质数,若 是质数,若 ,则 ,则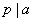 ; ;
(6)(带余除法)设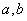 为整数, 为整数, ,则存在整数 ,则存在整数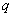 和 和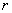 ,使得 ,使得 ,其中 ,其中 ,并且 ,并且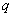 和 和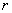 由上述条件唯一确定;整数 由上述条件唯一确定;整数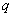 被称为 被称为 被 被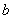 除得的(不完全)商,数 除得的(不完全)商,数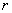 称为 称为 被 被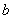 除得的余数。注意: 除得的余数。注意: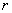 共有 共有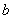 种可能的取值:0,1,……, 种可能的取值:0,1,……, 。若 。若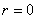 ,即为 ,即为 被 被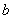 整除的情形; 整除的情形;
易知,带余除法中的商实际上为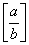 (不超过 (不超过 的最大整数),而带余除法的核心是关于余数 的最大整数),而带余除法的核心是关于余数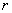 的不等式: 的不等式: 。证明 。证明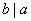 的基本手法是将 的基本手法是将 分解为 分解为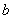 与一个整数之积,在较为初级的问题中,这种数的分解常通过在一些代数式的分解中取特殊值而产生,下面两个分解式在这类论证中应用很多,见例1、例2。 与一个整数之积,在较为初级的问题中,这种数的分解常通过在一些代数式的分解中取特殊值而产生,下面两个分解式在这类论证中应用很多,见例1、例2。
若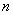 是正整数,则 是正整数,则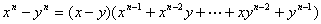 ; ;
若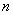 是正奇数,则 是正奇数,则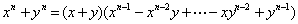 ;(在上式中用 ;(在上式中用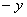 代 代 ) )
(7)如果在等式 中取去某一项外,其余各项均为 中取去某一项外,其余各项均为 的倍数,则这一项也是 的倍数,则这一项也是 的倍数; 的倍数;
(8)n个连续整数中,有且只有一个是n的倍数;
(9)任何n个连续的整数之积一定是n!的倍数,特别地,三个连续的正整数之积能被6整除;
2.奇数、偶数有如下性质:
(1)奇数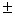 奇数=偶数,偶数 奇数=偶数,偶数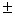 偶数=偶数,奇数 偶数=偶数,奇数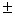 偶数=奇数,偶数 偶数=奇数,偶数 偶数=偶数,奇数 偶数=偶数,奇数 偶数=偶数,奇数 偶数=偶数,奇数 奇数=奇数;即任意多个偶数的和、差、积仍为偶数,奇数个奇数的和、差仍为奇数,偶数个奇数的和、差为偶数,奇数与偶数的和为奇数,和为偶数; 奇数=奇数;即任意多个偶数的和、差、积仍为偶数,奇数个奇数的和、差仍为奇数,偶数个奇数的和、差为偶数,奇数与偶数的和为奇数,和为偶数;
(2)奇数的平方都可以表示成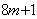 的形式,偶数的平方可以表示为 的形式,偶数的平方可以表示为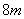 或 或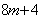 的形式; 的形式;
(3)任何一个正整数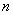 ,都可以写成 ,都可以写成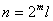 的形式,其中 的形式,其中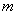 为负整数, 为负整数, 为奇数。 为奇数。
(4)若有限个整数之积为奇数,则其中每个整数都是奇数;若有限个整数之积为偶数,则这些整数中至少有一个是偶数;两个整数的和与差具有相同的奇偶性;偶数的平方根若是整数,它必为偶数。
3.完全平方数及其性质
能表示为某整数的平方的数称为完全平方数,简称平方数。平方数有以下性质与结论:
(1)平方数的个位数字只可能是0,1,4,5,6,9;
(2)偶数的平方数是4的倍数,奇数的平方数被8除余1,即任何平方数被4除的余数只有可能是0或1;
(3)奇数平方的十位数字是偶数;
(4)十位数字是奇数的平方数的个位数一定是6;
(5)不能被3整除的数的平方被3除余1,能被3整数的数的平方能被3整除。因而,平方数被9也合乎的余数为0,1,4,7,且此平方数的各位数字的和被9除的余数也只能是0,1,4,7;
(6)平方数的约数的个数为奇数;
(7)任何四个连续整数的乘积加1,必定是一个平方数。
(8)设正整数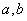 之积是一个正整数的 之积是一个正整数的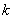 次方幂( 次方幂(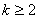 ),若( ),若(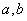 )=1,则 )=1,则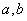 都是整数的 都是整数的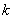 次方幂。一般地,设正整数 次方幂。一般地,设正整数 之积是一个正整数的 之积是一个正整数的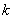 次方幂( 次方幂(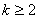 ),若 ),若 两两互素,则 两两互素,则 都是正整数的k次方幂。 都是正整数的k次方幂。
4.整数的尾数及其性质
整数 的个位数也称为整数 的个位数也称为整数 的尾数,并记为 的尾数,并记为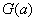 。 。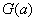 也称为尾数函数,尾数函数具有以下性质: 也称为尾数函数,尾数函数具有以下性质:
(1)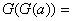 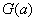 ;(2) ;(2) = =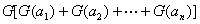 ; ;
(3)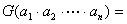  ;(4) ;(4) ; ;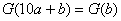 ; ;
(5)若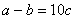 ,则 ,则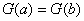 ;(6) ;(6)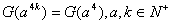 ; ;
(7) ; ;
(8)
5.整数整除性的一些数码特征(即常见结论)
(1)若一个整数的未位数字能被2(或5)整除,则这个数能被2(或5)整除,否则不能;
(2)一个整数的数码之和能被3(或9)整除,则这个数能被3(或9)整除,否则不能;
(3)若一个整数的未两位数字能被4(或25)整除,则这个数能被4(或25)整除,否则不能;
(4)若一个整数的未三位数字能被8(或125)整除,则这个数能被8(或125)整除,否则不能;
(5)若一个整数的奇位上的数码之和与偶位上的数码之和的差是11的倍数,则这个数能被11整除,否则不能。
6.质数与合数及其性质
1.正整数分为三类:(1)单位数1;(2)质数(素数):一个大于1的正整数,如果它的因数只有1和它本身,则称为质(素)数;(3)如果一个自然数包含有大于1而小于其本身的因子,则称这个自然数为合数。
2.有关质(素)数的一些性质
(1)若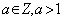 ,则 ,则 的除1以外的最小正因数 的除1以外的最小正因数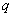 是一个质(素)数。如果 是一个质(素)数。如果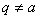 ,则 ,则 ; ;
(2)若 是质(素)数, 是质(素)数, 为任一整数,则必有 为任一整数,则必有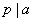 或( 或( )=1; )=1;
(3)设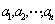 为 为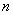 个整数, 个整数, 为质(素)数,且 为质(素)数,且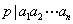 ,则 ,则 必整除某个 必整除某个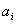 ( (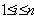 ); );
(4)(算术基本定理)任何一个大于1的正整数 ,能唯一地表示成质(素)因数的乘积(不计较因数的排列顺序); ,能唯一地表示成质(素)因数的乘积(不计较因数的排列顺序);
(5)任何大于1的整数 能唯一地写成 能唯一地写成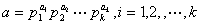 ① 的形式,其中 ① 的形式,其中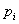 为质(素)数( 为质(素)数(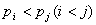 )。上式叫做整数 )。上式叫做整数 的标准分解式; 的标准分解式;
(6)若 的标准分解式为①, 的标准分解式为①, 的正因数的个数记为 的正因数的个数记为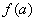 ,则 ,则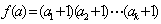 。 。
典例分析
例1.证明: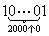 被1001整除。 被1001整除。
证明:
所以 整除 整除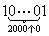 。 。
例2.对正整数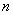 ,记 ,记 为 为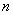 的十进制表示中数码之和。证明: 的十进制表示中数码之和。证明: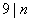 的充要条件是 的充要条件是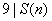 。 。
证明:设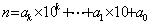 (这里 (这里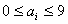 ,且 ,且 ),则 ),则 ,于是有 ,于是有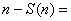  ① ①
对于 ,知 ,知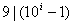 ,故①式右端 ,故①式右端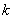 个加项中的每一个都是9的倍数,从而由整除的性质可知它们的和也能被9整除,即 个加项中的每一个都是9的倍数,从而由整除的性质可知它们的和也能被9整除,即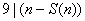 。由此可易推出结论的两个方面。 。由此可易推出结论的两个方面。
例3.设 是一个奇数,证明L对于任意正整数 是一个奇数,证明L对于任意正整数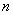 ,数 ,数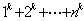 不能被 不能被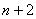 整除。 整除。
证明: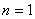 时,结论显然成立。设 时,结论显然成立。设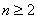 ,记所说的和为A,则: ,记所说的和为A,则:
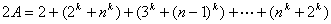 。 。
由k是正奇数,从而结于每一个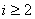 ,数 ,数 被 被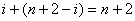 整除,故 整除,故 被 被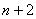 除得余数为2,从而A不可能被 除得余数为2,从而A不可能被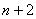 整除(注意 整除(注意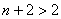 )。 )。
例4.设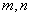 是正整数, 是正整数,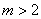 ,证明:( ,证明:( ) )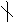 ( (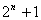 )。 )。
证明:首先,当 时,易知结论成立。事实上, 时,易知结论成立。事实上,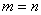 时,结论平凡;当 时,结论平凡;当 时,结果可由 时,结果可由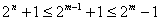 推出来(注意 推出来(注意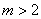 )。 )。
最后,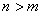 的情形可化为上述特殊情形:由带余除法 的情形可化为上述特殊情形:由带余除法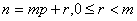 而 而 ,由于 ,由于 ,从而由若 ,从而由若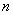 是正整数,则 是正整数,则 知 知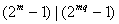 ;而 ;而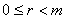 ,故由上面证明了的结论知 ,故由上面证明了的结论知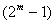 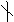  (注意 (注意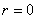 时结论平凡),从而当 时结论平凡),从而当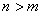 时,也有( 时,也有( ) ) ( (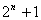 )。这就证明了本题的结论。 )。这就证明了本题的结论。
例5.设正整数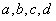 满足 满足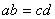 ,证明: ,证明: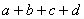 不是质(素)数。 不是质(素)数。
证法一:由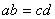 ,可设 ,可设 其中 其中 。由 。由 意味着有理数 意味着有理数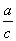 的分子、分母约去了某个正整数 的分子、分母约去了某个正整数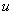 后得既约分数 后得既约分数 ,因此, ,因此,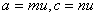 ① ①
同理,存在正整数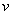 使得 使得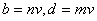 ② ②
因此,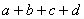 = =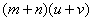 是两个大于1的整数之积,从而不是素数。 是两个大于1的整数之积,从而不是素数。
注:若正整数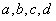 适合 适合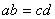 ,则 ,则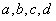 可分解为①及②的形式,这一结果在某些问题的解决中很有作用。 可分解为①及②的形式,这一结果在某些问题的解决中很有作用。
证法二:由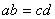 ,得 ,得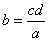 ,因此 ,因此 ,因为 ,因为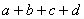 是整数,故 是整数,故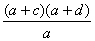 也是整数。 也是整数。
若它是一个素数,设为 ,则由 ,则由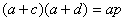 ③ ③
可见 整除 整除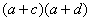 ,从而素数 ,从而素数 整除 整除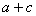 或 或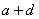 。不妨设 。不妨设 | |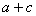 ,则 ,则 ,结合③推出 ,结合③推出 ,而这是不可能的(因为 ,而这是不可能的(因为 )。 )。
例6.求出有序整数对(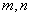 )的个数,其中 )的个数,其中 , , , , 是完全平方数。 (1999年美国数学邀请赛试题) 是完全平方数。 (1999年美国数学邀请赛试题)
解:由于 , , 可得: 可得:
 < <  。 。
又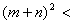  ,于是 ,于是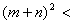  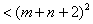
若 是完全平方数,则必有 是完全平方数,则必有 = = 。 。
然而 = = 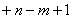 ,于是必有 ,于是必有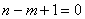 ,即 ,即 ,此时 ,此时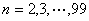 , ,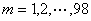 。所以所求的有序整数对( 。所以所求的有序整数对(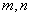 )共有98对: )共有98对:
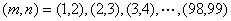 。 。
例7.证明:若正整数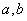 满足 满足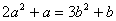 ,则 ,则 和 和 都是完全平方数。 (2006年山东省第二届夏令营试题) 都是完全平方数。 (2006年山东省第二届夏令营试题)
证法一:已知关系式即为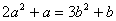 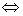 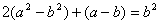
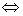 ( ( )( )( )= )= ① ①
若 (或者说 (或者说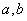 中有一个为0时),结论显然。 中有一个为0时),结论显然。
不妨设 且 且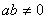 ,令 ,令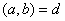 ,则 ,则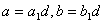 , ,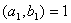
从而 = = ,将其代入①得 ,将其代入①得 ② ②
因为  ,所以 ,所以 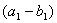 ,从而 ,从而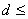  ; ;
而②式又可写成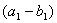 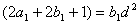 ; ;
因为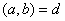 且 且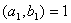 ,所以 ,所以 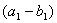
所以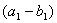  ,从而 ,从而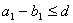 。 。
所以 ,所以 ,所以 = = ,从而 ,从而 为完全平方数。 为完全平方数。
所以 也是完全平方数。 也是完全平方数。
证法二:已知关系式即为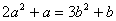 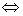 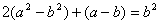
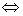 ( ( )( )( )= )= ① ①
论证的关键是证明正整数 与 与 互素。 互素。
记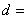 ( ( , , )。若 )。若 ,则 ,则 有素因子 有素因子 ,从而由①知 ,从而由①知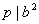 。因为 。因为 是素数,故 是素数,故 ,结合 ,结合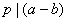 知 知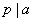 ,从而由 ,从而由  得 得 1,这是不可能的。故 1,这是不可能的。故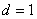 ,从而由①推知正整数 ,从而由①推知正整数 与 与 都是完全平方数。 都是完全平方数。
例8.证明不存在正整数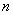 ,使2n2+1,3n2+1,6n2+1都是完全平方数。 ,使2n2+1,3n2+1,6n2+1都是完全平方数。
证明:假设存在这样的正整数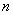 ,使2n2+1,3n2+1,6n2+1都是完全平方数,那么 ,使2n2+1,3n2+1,6n2+1都是完全平方数,那么
(2n2+1)(3n2+1)(6n2+1)也必定是完全平方数。
而(2n2+1)(3n2+1)(6n2+1)=36n6+36n4+11n2+1;
 36n6+36n4+9n2; 36n6+36n4+9n2;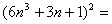 36n6+36n4+12n3+9n2+6n+1; 36n6+36n4+12n3+9n2+6n+1;
所以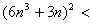 (2n2+1)(3n2+1)(6n2+1)< (2n2+1)(3n2+1)(6n2+1)<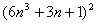 与(2n2+1)(3n2+1)(6n2+1)为完全平方数矛盾。 与(2n2+1)(3n2+1)(6n2+1)为完全平方数矛盾。
例9.数列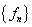 的通项公式为 的通项公式为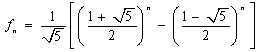 , ,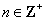 . .
记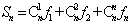 ,求所有的正整数 ,求所有的正整数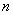 ,使得 ,使得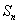 能被8整除.(2005年上海竞赛试题) 能被8整除.(2005年上海竞赛试题)
解:记
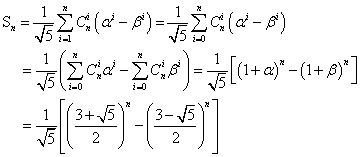
注意到 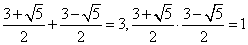 ,可得 ,可得
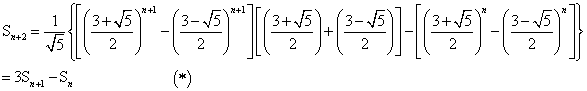
因此,Sn+2除以8的余数,完全由Sn+1、Sn除以8的余数确定
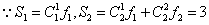 ,故由(*)式可以算出 ,故由(*)式可以算出 各项除以8的余数依次是1,3,0,5,7,0,1,3,……,它是一个以6为周期的数列,从而 各项除以8的余数依次是1,3,0,5,7,0,1,3,……,它是一个以6为周期的数列,从而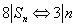
故当且仅当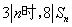
练习题
1.证明:如果 和 和 都是大于3的素数,则6是 都是大于3的素数,则6是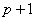 的因子。 的因子。
证明:因为 是奇数,所以2是 是奇数,所以2是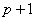 的因子。又因为 的因子。又因为 , ,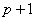 , , 除以3的余数各不相同,而 除以3的余数各不相同,而 与 与 都不能被3整数。于是6是 都不能被3整数。于是6是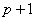 的因子。 的因子。
2.设 ,证明: ,证明: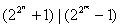 ; ;
解:由  ,故 ,故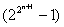 |( |( )。 )。
又因为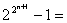   ,从而 ,从而 | |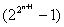 ,于是由整除的性质知 ,于是由整除的性质知
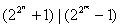 。 。
3.证明:对于任意正整数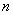 ,数 ,数 不能被 不能被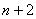 整除。 整除。
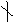 证明:只需证2( 证明:只需证2(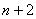 )2( )2(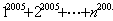 )即可。 )即可。
因为若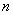 是正整数,则 是正整数,则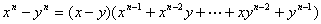 ; ;
若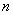 是正奇数,则 是正奇数,则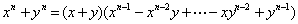 ; ;
故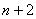 | | ; ;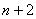 | | ,……, ,……, 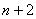 | |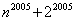
所以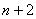 |2( |2( )。 )。
  又因为 又因为 ,所以 ,所以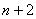 2,所以 2,所以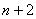 2( 2( )+2 )+2
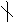 即( 即(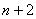 )2( )2(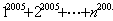 )命题得证。 )命题得证。
4.已知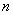 为正奇数,求证: 为正奇数,求证: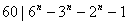 。 。
证明:因为若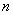 是正整数,则 是正整数,则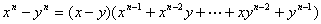 ; ;
若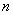 是正奇数,则 是正奇数,则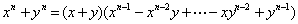 ; ;
所以 , ,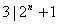 ,从而 ,从而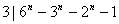 ; ;
 , ,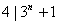 ,从而 ,从而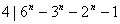 ; ;
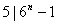 , ,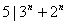 ,从而 ,从而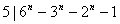 ; ;
又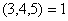 且 且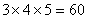 ,所以 ,所以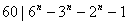 。 。
5.设a、b、c为满足不等式1<a<b<c的整数,且(ab-1)(bc-1)(ca-1)能被abc整除,求所有可能数组(a,b,c).(1989年上海竞赛试题)
解 ∵(ab-1)(bc-1)(ca-1)
=a2b2c2-abc(a+b+c)+ab+ac+bc-1,①
∵abc|(ab-1)(bc-1)(ca-1).
∴存在正整数k,使ab+ac+bc-1=kabc, ②
k=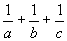 < < < <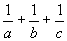 < < < <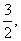 ∴k=1. ∴k=1.
若a≥3,此时1=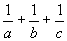 - - < <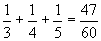 矛盾. 矛盾.
已知a>1. ∴只有a=2.
当a=2时,代入②中得2b+2c-1=bc,即 1= < <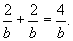
∴0<b<4,知b=3,从而易得c=5.
说明:在此例中通过对因数k的范围讨论,从而逐步确定a、b、c是一项重要解题技巧.
(责任编辑:admin) |

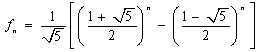 ,
,