基础知识
1.数列的概念
定义1. 按照某一法则,给定了第1个数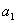 ,第2个数 ,第2个数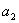 ,………,对于正整数 ,………,对于正整数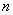 有一个确定的数 有一个确定的数 ,于是得到一列有次序的数 ,于是得到一列有次序的数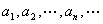 我们称它为数列,用符号 我们称它为数列,用符号 表示。数列中的每项称为数列的项,第 表示。数列中的每项称为数列的项,第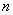 项 项 称为数列的一般项,又称为数列 称为数列的一般项,又称为数列 的通项。 的通项。
定义2.当一个数列的项数为有限个时,称这个数列为有限数列;当一个数列的项数为无限时,则称这个数列为无限数列。
定义3.对于一个数列,如果从第2项起,每一项都不小于它的前一项,即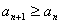 ,这样的数列称为递增数列;如果从第2项起,每一项都不大于它的前一项,即 ,这样的数列称为递增数列;如果从第2项起,每一项都不大于它的前一项,即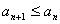 ,这样的数列称为递减数列。 ,这样的数列称为递减数列。
定义4.如果数列的每一项的绝对值都小于某一个正数,即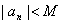 ,其中 ,其中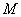 是某一个正数,则称这样的数列为有界数列,否则就称为是无界数列。 是某一个正数,则称这样的数列为有界数列,否则就称为是无界数列。
定义5.如果在数列 中,项数 中,项数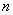 与 与 具有如下的函数关系: 具有如下的函数关系: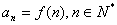 ,则称这个关系为数列 ,则称这个关系为数列 的通项公式。 的通项公式。
2.等差数列
定义6.一般地,如果一个数列从第2项起,每一项与它前一项的差等于同一个常数,这个数列就叫做等差数列,这个常数叫做公差,常用字母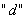 表示。 表示。
等差数列具有以下几种性质:
(1)等差数列的通项公式: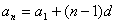 或 或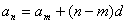 ; ;
(2)等差数列的前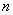 项和公式: 项和公式: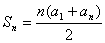 或 或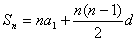 ; ;
(3)公差非零的等差数列的通项公式为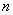 的一次函数; 的一次函数;
(4)公差非零的等差数列的前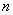 项和公式是关于 项和公式是关于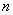 不含有常数项的二次函数; 不含有常数项的二次函数;
(5)设 是等差数列,则 是等差数列,则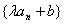 ( (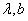 是常数)是公差为 是常数)是公差为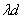 的等差数列; 的等差数列;
(6)设 , ,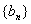 是等差数列,则 是等差数列,则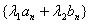 ( (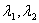 是常数)也是等差数列; 是常数)也是等差数列;
(7)设 , ,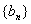 是等差数列,且 是等差数列,且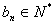 ,则 ,则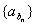 也是等差数列(即等差数列中等距离分离出的子数列仍为等差数列); 也是等差数列(即等差数列中等距离分离出的子数列仍为等差数列);
(8)若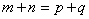 ,则 ,则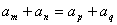 ;特别地,当 ;特别地,当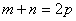 时, 时,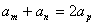 ; ;
(9)设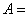 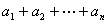 , ,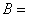 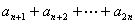 , ,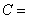 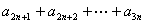 ,则有 ,则有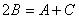 ; ;
(10)对于项数为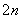 的等差数列 的等差数列 ,记 ,记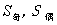 分别表示前 分别表示前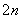 项中的奇数项的和与偶数项的和,则 项中的奇数项的和与偶数项的和,则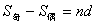 , ,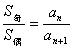 ; ;
(11)对于项数为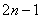 的等差数列 的等差数列 ,有 ,有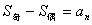 , ,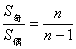 ; ;
(12) 是等差数列的前 是等差数列的前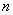 项和,则 项和,则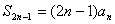 ; ;
(13)其他衍生等差数列:若已知等差数列 ,公差为 ,公差为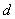 ,前 ,前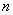 项和为 项和为 ,则 ,则
①.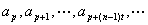 为等差数列,公差为 为等差数列,公差为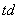 ; ;
②.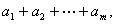 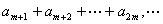 (即 (即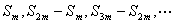 )为等差数列,公差 )为等差数列,公差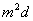 ; ;
③.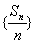 (即 (即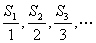 )为等差数列,公差为 )为等差数列,公差为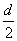 . .
3.等比数列
定义7.一般地,如果有一个数列从第2项起,每一项与它的前一项的比等于现中一个常数,那么这个数列就叫做等比数列,这个常数叫做公比;公比通常用字母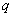 表示( 表示(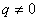 ),即。 ),即。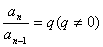
等比数列具有以下性质:
(1)等比数列的通项公式: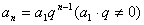 或 或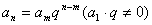 ; ;
(2)等比数列的前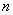 项和公式: 项和公式: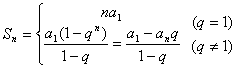 ; ;
(3)等比中项: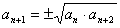 ; ;
(4)无穷递缩等比数列各项公式:对于等比数列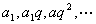 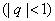 的前 的前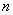 项和,当 项和,当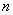 无限增大时的极限,叫做这个无穷递缩数列的各项的和,记为 无限增大时的极限,叫做这个无穷递缩数列的各项的和,记为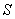 ,即 ,即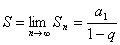 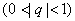 ; ;
(5)设 是等比数列,则 是等比数列,则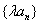 ( (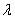 是常数), 是常数),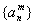 仍成等比数列; 仍成等比数列;
(6)设 , ,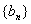 是等比数列,则 是等比数列,则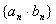 也是等比数列; 也是等比数列;
(7)设 是等比数列, 是等比数列,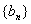 是等差数列,且 是等差数列,且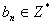 则 则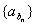 也是等比数列(即等比数列中等距离分离出的子数列仍为等比数列); 也是等比数列(即等比数列中等距离分离出的子数列仍为等比数列);
(8)设 是正项等比数列,则 是正项等比数列,则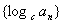 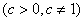 是等差数列; 是等差数列;
(9)若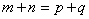 ,则 ,则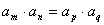 ;特别地,当 ;特别地,当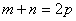 时, 时,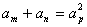 ; ;
(10)设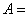 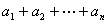 , ,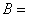 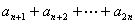 , ,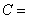 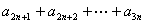 ,则有 ,则有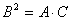 ; ;
(11)其他衍生等比数列:若已知等比数列 ,公比为 ,公比为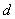 ,前 ,前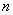 项和为 项和为 ,则 ,则
①.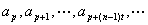 为等比数列,公比为 为等比数列,公比为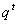 ; ;
②.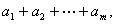 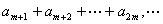 (即 (即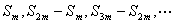 )为等比数列,公比为 )为等比数列,公比为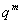 ; ;
典例分析
例1.设等差数列的首项与公差均为非负整数,项数不小于3,且各项之和为972,则这样的数列有_____________个。
解:设等差数列的首项为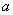 ,公差为 ,公差为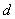 。由已知有 。由已知有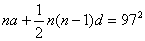 ,即 ,即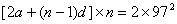 。又因为 。又因为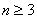 ,所以 ,所以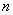 只可能取 只可能取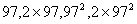 ,又因为 ,又因为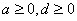 且 且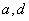 均为整数,故 均为整数,故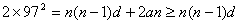 ; ;
若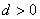 ,由于 ,由于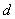 为正数,则 为正数,则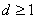 ,即 ,即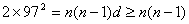 ,故 ,故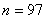 ,这时有 ,这时有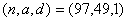 或 或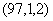 ; ;
若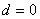 ,则 ,则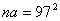 ,这时有 ,这时有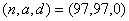 或 或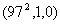 。 。
例2.设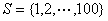 ,A是S的三元子集,满足:A中元素可以组成等差数列,那么这样的三元子集有___________个。 ,A是S的三元子集,满足:A中元素可以组成等差数列,那么这样的三元子集有___________个。
解:若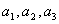 成等差数列,则 成等差数列,则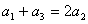 ,从而首未两项奇偶相同,且首未两项一旦确定,那么等差数列也就随之确定了。但是值得注意的是,虽然 ,从而首未两项奇偶相同,且首未两项一旦确定,那么等差数列也就随之确定了。但是值得注意的是,虽然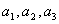 成等差数列时, 成等差数列时,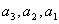 也成等差数列,但它们所对应的是同一个集合A={ 也成等差数列,但它们所对应的是同一个集合A={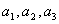 }。 }。
将S按数的奇偶性分成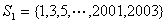 与 与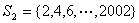 两个子集。 两个子集。
从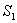 中取出两个数作为等差数列的首未两项,共有 中取出两个数作为等差数列的首未两项,共有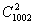 种不同的取法; 种不同的取法;
从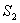 中取出两个数作为等差数列的首未两项,共有 中取出两个数作为等差数列的首未两项,共有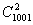 种不同的取法; 种不同的取法;
所以共有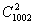 + +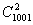 种不同的取法。 种不同的取法。
例3.设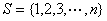 ,A为至少含有两项且公差为正的等差数列,其项都在S中,且添加S的其它元素于A后均不能构成与A有相同公差的等差数列,求这种A的个数(这里只有两项的数列也看作是等差数列)(1991年全国高中数学联赛二试第一题) ,A为至少含有两项且公差为正的等差数列,其项都在S中,且添加S的其它元素于A后均不能构成与A有相同公差的等差数列,求这种A的个数(这里只有两项的数列也看作是等差数列)(1991年全国高中数学联赛二试第一题)
分析:可先对特殊的n(如n=1,2,3)通过列举法求出A的个数,然后总结规律,找出 的递推关系,从而解决问题;也可以就A的公差 的递推关系,从而解决问题;也可以就A的公差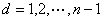 时,讨论A的个数。 时,讨论A的个数。
解法一:设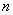 元素集 元素集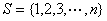 中满足条件的A有 中满足条件的A有 个,则 个,则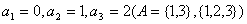 , ,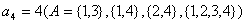 ,……如此下去,可以发现 ,……如此下去,可以发现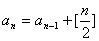 。 。
事实上,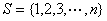 比 比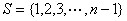 的A增加的公差为 的A增加的公差为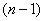 的1个,公差为 的1个,公差为 的1个,……,公差为 的1个,……,公差为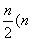 为偶数)或 为偶数)或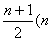 为奇数)的增加1个,共增加 为奇数)的增加1个,共增加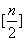 个。 个。
由 的递推公式可得 的递推公式可得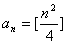 个。 个。
解法二:设A的公差为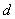 ,则 ,则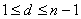 ,分为两种情况讨论: ,分为两种情况讨论:
(1)当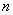 为偶数时,则当 为偶数时,则当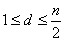 时,公差为 时,公差为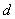 的A有 的A有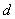 个,当 个,当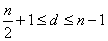 时,公差为d的A有 时,公差为d的A有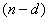 个,故当n为偶数时,这种A共有 个,故当n为偶数时,这种A共有
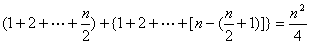 个; 个;
(2)当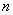 为奇数时,则当 为奇数时,则当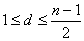 时,公差为 时,公差为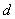 的A有 的A有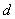 个,当 个,当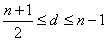 时,公差为d的A有 时,公差为d的A有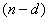 个,故当n为奇数时,这种A共有 个,故当n为奇数时,这种A共有
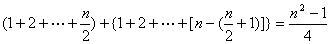 个; 个;
综合(1)(2)得,所求的A共有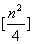 个。 个。
例4.将数列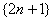 依次按每一项,两项,三项,四项循环分成(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43)……,则第100个括号内的各数之和是__________________。 依次按每一项,两项,三项,四项循环分成(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,31,33),(35,37,39,41),(43)……,则第100个括号内的各数之和是__________________。
解:每循环一次记为一组,则第100个括号是第25组的第4个括号。而每组中第四个括号内的各数之和构成以72为首项,以80为公差的等差数列,故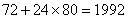 为所求。 为所求。
例5.设数列 是等差数列, 是等差数列,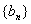 是等比数列,且 是等比数列,且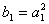 , ,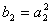 , ,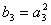 ( (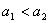 ),又 ),又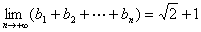 ,试求数列 ,试求数列 的首项与公差。(2000年全国高中数学联赛一试第13题) 的首项与公差。(2000年全国高中数学联赛一试第13题)
分析;题中两个基本量 中的首项 中的首项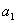 和公差 和公差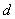 是所需求的。利用 是所需求的。利用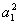 , ,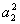 , ,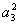 成等比数列和给定的极限可列出两个方程,但需注意极限存在的条件。 成等比数列和给定的极限可列出两个方程,但需注意极限存在的条件。
解:设所求的首项为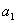 ,公差为 ,公差为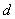 。因为 。因为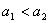 ,故 ,故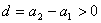 ;又因为 ;又因为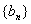 成等比数列,故 成等比数列,故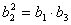 ,即 ,即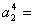 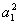 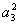 ,即 ,即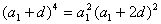 ,化简得: ,化简得: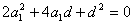 ,解得 ,解得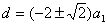 ,而 ,而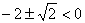 ,故 ,故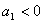 ; ;
若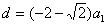 ,则 ,则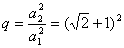 ;若 ;若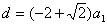 ,则 ,则 ; ;
但是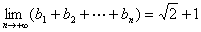 存在,可知 存在,可知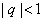 ,于是 ,于是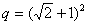 不合题意,从而只有 不合题意,从而只有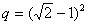 。于是由 。于是由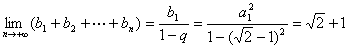
解得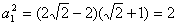 ,所以 ,所以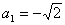 , ,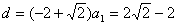
故数列 的首项与公差分别为 的首项与公差分别为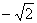 和 和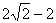 。 。
例6.若复数列 的通项公式为 的通项公式为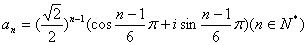
(1)将数列 的各项与复平面上的点对应,问从第几项起,以后所有的各项对应的点都落在圆 的各项与复平面上的点对应,问从第几项起,以后所有的各项对应的点都落在圆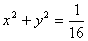 的内部; 的内部;
(2)将数列 中的实数项按原来的顺序排成一个新数列 中的实数项按原来的顺序排成一个新数列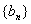 ,求数列 ,求数列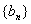 的通项及所有项的和。 的通项及所有项的和。
解:(1)设数列 的各项在复平面上对应的点的坐标为 的各项在复平面上对应的点的坐标为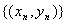 ,则 ,则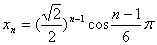 , ,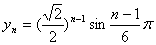 。 。
要使点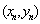 落在圆 落在圆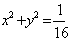 的内部, 的内部,
只需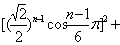 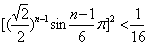 ,得 ,得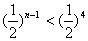
即 ,故从第6项起,以后每一项都落在圆 ,故从第6项起,以后每一项都落在圆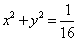 的内部。 的内部。
(2)要使数列 中的项为实数,则 中的项为实数,则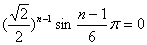 ,得 ,得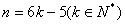 , ,
因此数列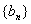 的通项公式为 的通项公式为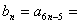 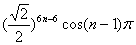 , ,
所以 ,且 ,且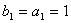
故数列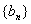 是首项为1,公比为 是首项为1,公比为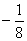 的无穷递缩数列,从而数列 的无穷递缩数列,从而数列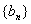 的所有项的和为: 的所有项的和为: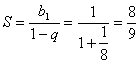 。 。
例7.已知整数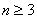 , ,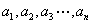 是1,2,3,……,n的一个排列,求证: 是1,2,3,……,n的一个排列,求证: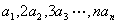 不可能构成一个等差数列,也不可能构成一个等比数列。(2006年山东省第二届夏令营试题) 不可能构成一个等差数列,也不可能构成一个等比数列。(2006年山东省第二届夏令营试题)
证明:若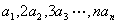 构成一个等差数列,设其公差为 构成一个等差数列,设其公差为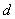 ,则 ,则 , ,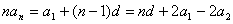 ,所以 ,所以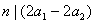 。 。
而 ,因为 ,因为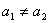 ,所以 ,所以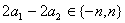
所以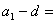 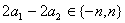 。 。
于是当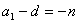 时,则 时,则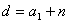 ,于是 ,于是
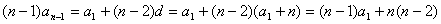
所以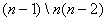 ,矛盾! ,矛盾!
当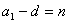 时,则 时,则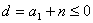 , 又因为 , 又因为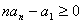 所以 所以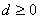 ,从而 ,从而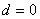 。 。
所以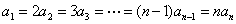 ,所以 ,所以 ,从而 ,从而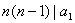 ,矛盾! ,矛盾!
从而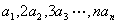 不可能构成一个等差数列。 不可能构成一个等差数列。
下证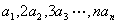 不可能构成一个等比数列。 不可能构成一个等比数列。
若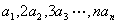 构成了一个等比数列,考虑最后三项。 构成了一个等比数列,考虑最后三项。
有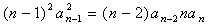 ,所以 ,所以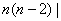 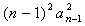 。 。
而(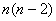 , ,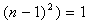 ,所以 ,所以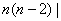 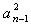 ; ;
当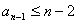 时,显然 时,显然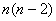 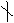  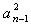 ; ;
当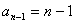 时,显然 时,显然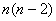 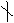   ; ;
当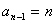 时,有 时,有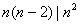 ,知 ,知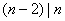 ,所以 ,所以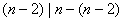 即 即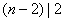 ,所以 ,所以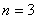 或4; 或4;
当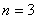 时, 时,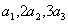 只能为1,6,6或2,6,3,但这两个都不是等比数列; 只能为1,6,6或2,6,3,但这两个都不是等比数列;
当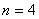 时, 时,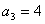 ,所以 ,所以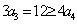 故 故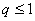 ;又因为 ;又因为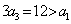 ,所以 ,所以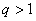 矛盾! 矛盾!
所以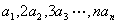 也不可能构成一个等比数列。 也不可能构成一个等比数列。
例8.正整数序列 按以下方式构成: 按以下方式构成: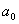 为某个正数,如果 为某个正数,如果 能被5整除,则 能被5整除,则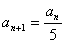 ;如果 ;如果 不能被5整除,,则 不能被5整除,,则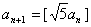 。证明:数列{ 。证明:数列{ }自某一项起,以后各项都不是5的倍数。(2006年山东省第二届夏令营试题) }自某一项起,以后各项都不是5的倍数。(2006年山东省第二届夏令营试题)
证明:首先证明 中一定在存在相邻的两项,它们都不是5的倍数。 中一定在存在相邻的两项,它们都不是5的倍数。
(反证)若不然,数列 中任意的两项都是5的倍数。 中任意的两项都是5的倍数。
若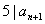 ,则 ,则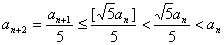 ; ;
若5 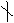 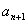 ,则 ,则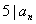 ,从而 ,从而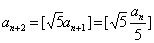 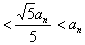 ; ;
所以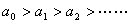 矛盾!(因为某个正数,不可能大于无穷多个正整数) 矛盾!(因为某个正数,不可能大于无穷多个正整数)
从而 中一定在相在相邻的两项,它们都不是5的倍数。 中一定在相在相邻的两项,它们都不是5的倍数。
设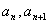 都不是5的倍数,则 都不是5的倍数,则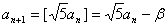 ,其中 ,其中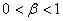 , ,
有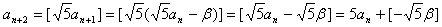
因为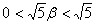 ,所以 ,所以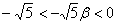 ,所以 ,所以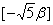 只能取 只能取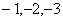 ,即 ,即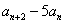 只能取 只能取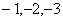 ,这说明 ,这说明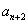 不是5的倍数。 不是5的倍数。
即从 起以后每一项都不是5的倍数。 起以后每一项都不是5的倍数。
例9.将与105互质的所有正整数从小到大排成数列,求这个数列的第三1000项。
解:设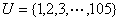 , ,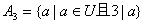 , ,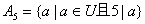 , ,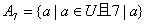
则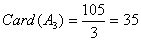 ; ;
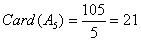 ; ;
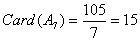 ; ;
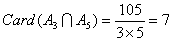 ; ;
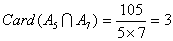 ; ;
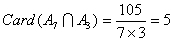 ; ;
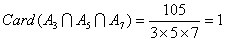 ,所以 ,所以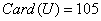 。 。
在1到105之间与105互质的数有
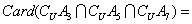 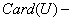 [ [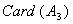
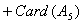 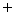 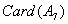 ]+[ ]+[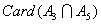 + +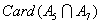 + + ] ]
-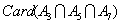 =105-(35+21+15)+(7+3+5)-1=48 =105-(35+21+15)+(7+3+5)-1=48
设将与105互质的数从小到大排列起来为数列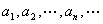 ,则 ,则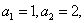 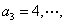
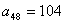 , ,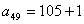 , ,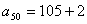 , ,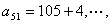 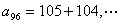
这是一个以48为周期的周数列,因为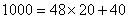
所以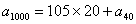 ; ;
而由于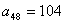 , ,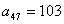 , ,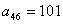 , ,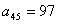 , ,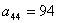 , ,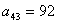 , ,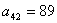 , ,
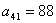 , ,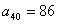 ; ;
所以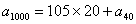 = =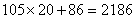 。 。
例10.数列 的定义如下: 的定义如下: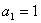 ,且当 ,且当 时,有 时,有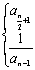 
现已知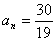 ,求正整数 ,求正整数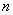 .(2006年山东省第二届夏令营试题) .(2006年山东省第二届夏令营试题)
解:由题设条件知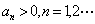 ,并由 ,并由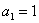 得当n为偶数时, 得当n为偶数时,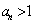 ,当n为奇数时, ,当n为奇数时,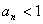 ; ;
由于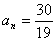 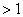 ,知n为偶数; ,知n为偶数;
所以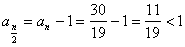 知 知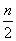 为奇数;所以 为奇数;所以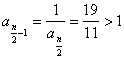 知 知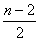 为偶数; 为偶数;
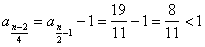 知 知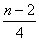 为奇数; 为奇数;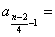 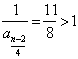 知 知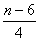 为偶数; 为偶数;
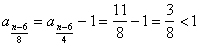 知 知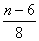 为奇数; 为奇数;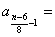 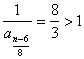 知 知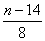 为偶数; 为偶数;
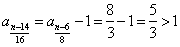 知 知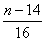 为偶数; 为偶数;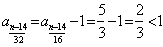 知 知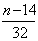 为奇数; 为奇数;
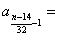 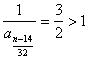 知 知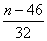 为偶数; 为偶数;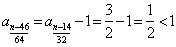 知 知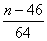 为奇数; 为奇数;
 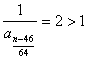 知 知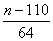 为偶数; 为偶数;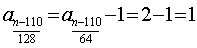
所以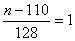 ,所以 ,所以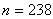 。 。
(责任编辑:admin) |
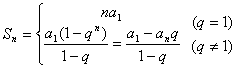 ;
;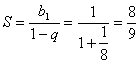 。
。
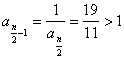 知
知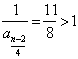 知
知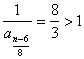 知
知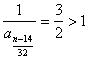 知
知 知
知