一、选择题
1.已知集合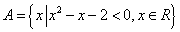 , ,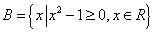 ,则 ,则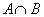 =( ) =( )
A. 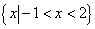 B. B. 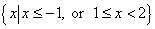 C. C. 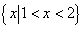 D. D. 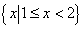
解: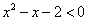 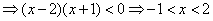
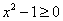 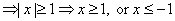 . .
从而可得 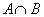 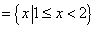 。 应选 D。 。 应选 D。
2. 当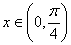 时,下面四个函数中最大的是( )。 时,下面四个函数中最大的是( )。
A. 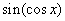 B. B. 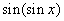 C. C. 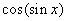 D. D. 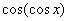
解:因为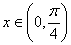 ,所以 ,所以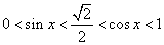 。 。
于是有 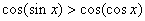 , ,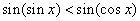 。 。
又因为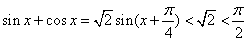 ,即 ,即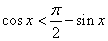 , ,
所以有 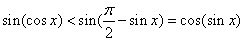 。 。
因此,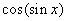 最大。 应选 C。 最大。 应选 C。
3. 已知椭圆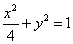 上一点A到左焦点的距离为 上一点A到左焦点的距离为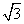 ,则点A到直线 ,则点A到直线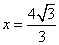 的距离为( ) 的距离为( )
A. 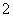 B. B. 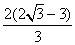 C. C. 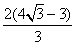 D. D. 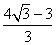
解: 设左右焦点为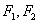 ,则 ,则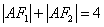 , ,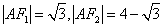 。 。
椭圆的离心率为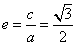 。而 。而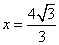 即为右准线, 即为右准线,
由定义得,A到直线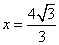 的距离等于 的距离等于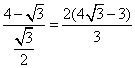 。 应选C。 。 应选C。
4.设非常值函数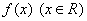 是一个偶函数,它的函数图像 是一个偶函数,它的函数图像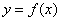 关于直线 关于直线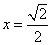 对称,则该函数是 ( ) 对称,则该函数是 ( )
A. 非周期函数 B.周期为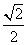 的周期函数 的周期函数
C. 周期为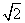 的周期函数 D. 周期为 的周期函数 D. 周期为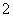 的周期函数 的周期函数
解:因为偶函数关于y轴对称,而函数图像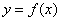 关于直线 关于直线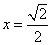 对称,则 对称,则
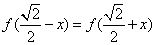 , ,
即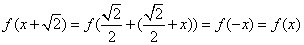 。 。
故该函数是周期为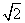 的周期函数。应选C。 的周期函数。应选C。
5. 如果 ,则使 ,则使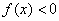 的 的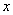 的取值范围为( ) 的取值范围为( )
A. 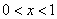 B. B. 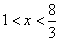 C. C. 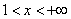 D. D. 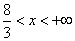
解:显然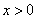 ,且 ,且 。 。
 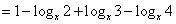 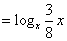 。 。
要使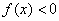 。当 。当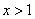 时, 时,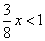 ,即 ,即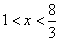 ;当 ;当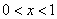 时, 时,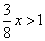 ,此时无解。 ,此时无解。
由此可得, 使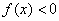 的 的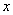 的取值范围为 的取值范围为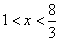 。 应选B。 。 应选B。
6. 设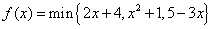 ,则 ,则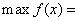 ( ) ( )
A. 1 B. 2 C. 3 D. 4
解: 作图比较容易得到 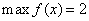 。 应选B。 。 应选B。
二、填空题
7. 已知平面上不共线的四点O,A,B,C。若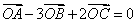 ,则 ,则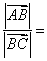 。 。
解:因为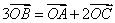 ,所以 ,所以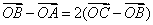 。于是有 。于是有 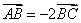 。 。
因此 。答案为:2。 。答案为:2。
8. 已知数列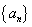 , ,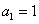 ,前n项部分和 ,前n项部分和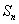 满足 满足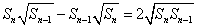 ,则 ,则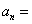 。 。
解: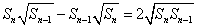 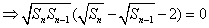
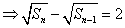 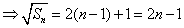 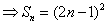 。 。
于是 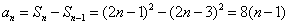 ,( ,(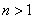 )。 )。
答案为: 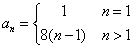 。 。
9.方程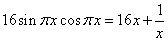 的解集合为 。 的解集合为 。
解: 当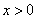 时, 时,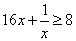 ,( ,( 取到等号)。 取到等号)。
而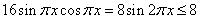 ,( ,(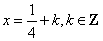 取到等号)。 取到等号)。
于是有 当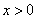 时,方程只有一个解 时,方程只有一个解 。 。
由于奇函数的性质,可知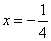 是方程的另一解。 是方程的另一解。
故方程的解集合为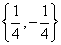 。 。
10.今天是星期天,再过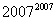 天后是星期 。 天后是星期 。
解: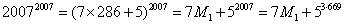
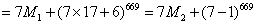
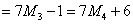
其中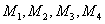 均为正整数。 因此答案为 星期六。 均为正整数。 因此答案为 星期六。
11. 从1至169的自然数中任意取出3个数构成以整数为公比的递增等比数列的取法有 种。
解:若取出的3个数构成递增等比数列 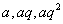 , ,
则有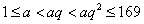 。 。
由此有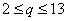 。当 。当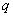 固定时,使三个数 固定时,使三个数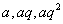 为整数的 为整数的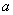 的个数记作 的个数记作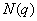 。 。
由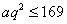 ,知 ,知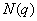 应是 应是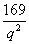 的整数部分。 的整数部分。
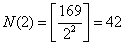 , ,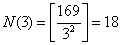 , ,
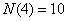 , ,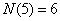 , ,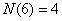 , ,
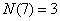 , ,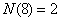 , ,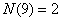 , ,
 . .
因此,取法共有 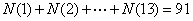 。 答案为 91 。 。 答案为 91 。
12. 整数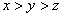 ,且 ,且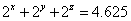 ,则 ,则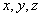 分别为 。 分别为 。
解:方程两边同乘以8,得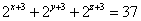 。 。
因为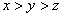 ,所以要使左边为奇数, ,所以要使左边为奇数,
只有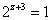 , ,
即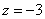 。 。
则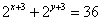 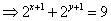 。 。
要使左边为奇数,只有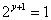 ,即 ,即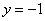 。 。
从而有 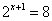 ,即 ,即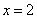 。故有 。故有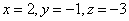 。 。
答案为 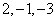 。 。
三、解答题
13. 设P,Q为圆周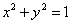 上的两动点,且满足与圆内一定点 上的两动点,且满足与圆内一定点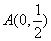 ,使 ,使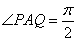 ,求过P和Q的两条切线的交点M的轨迹。 ,求过P和Q的两条切线的交点M的轨迹。
解法一:连接PQ,OM,由圆的切线性质知 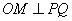 ,且PQ与OM交点E为PQ的中点。…………5分 ,且PQ与OM交点E为PQ的中点。…………5分
设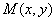 ,则 ,则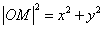 , ,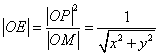 。从而得到E点的坐标为 。从而得到E点的坐标为
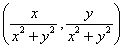 。 …………10分 。 …………10分
由于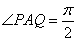 ,所以 ,所以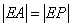 。又 。又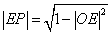 , ,
于是有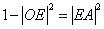 , ,
即有 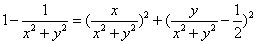 ………… 15分 ………… 15分
化简得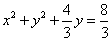 。 。
上述为以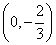 为圆心, 为圆心,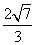 为半径的圆周。 …………20分 为半径的圆周。 …………20分
解法二: 设P,Q的坐标为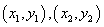 。由题意知,过P,Q的切线方程分别为 。由题意知,过P,Q的切线方程分别为
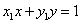 ………… ① ………… ①
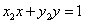 ………… ② ………… ②
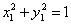 ………… ③ ………… ③
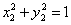 ………… ④ ………… 5分 ………… ④ ………… 5分
由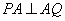 ,得 ,得
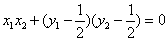 ………… ⑤ ………… ⑤
若①和②的交点仍记为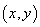 ,由此得到 ,由此得到
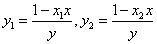 ( (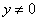 ) ………… 10分 ) ………… 10分
代入③和④,得
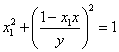 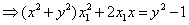
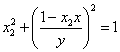 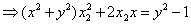
联立上述两式,即得
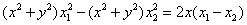 ………… 15分 ………… 15分
因为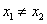 ,所以 ,所以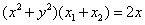 ,即 ,即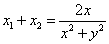 。 。
同理可得  。于是有 。于是有
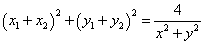
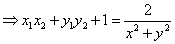
再由⑤式,推出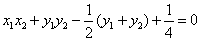 。 。
由上可得,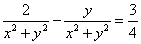 。 。
即有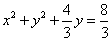 。 。
上述为以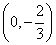 为圆心, 为圆心,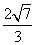 为半径的圆周。 …………20分 为半径的圆周。 …………20分
当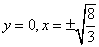 时,也符合题设所求的轨迹。 时,也符合题设所求的轨迹。
14. 设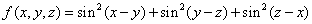 , ,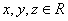 ,求 ,求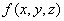 的最大值。 的最大值。
解: 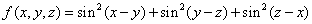
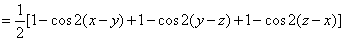 …………5分 …………5分
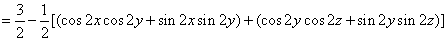
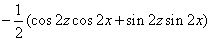 …………10分 …………10分
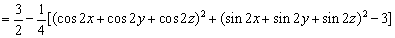
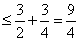 , …………15分 , …………15分
当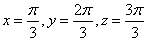 时,上式可以取到等号。 时,上式可以取到等号。
故函数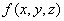 的最大值是 的最大值是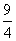 。…………20分 。…………20分
15. 设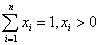 ,求证: ,求证: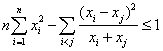 。 。
证明:因为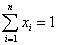 ,所以有 ,所以有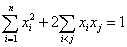 。 。
又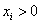 ,故有 ,故有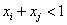 。…………10分 。…………10分
于是有
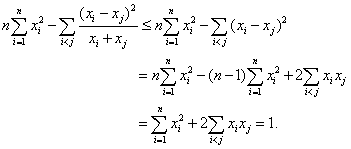
得证。 …………20分
(责任编辑:admin) |
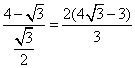 。 应选C。
。 应选C。 。答案为:2。
。答案为:2。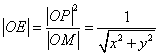 。从而得到E点的坐标为
。从而得到E点的坐标为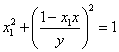
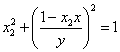
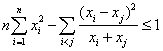 。
。