|
数学是研究现实世界的空间形式与数量关系的科学.数和形是客观事物不可分离的两个数学表象,两者既是对立的又是统一的.数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微.”数与形的对立统一主要表现在数与形的互相转化和互相结合上. 一、借“数”解“形” 一些几何问题,如果运用数与形结合的观点去考虑“形向数”的转化,通过数的运算和变式,求出相应的结果,则解题方法容易寻找.如采用代数方法、三角方法、解析方法、复数方法、向量方法去解决几何问题,解题思路比较明确,规律性强,不像几何证法须要特殊技巧,因此也就容易找到解题途径. (一)用代数法解几何问题 研究某些度量关系的几何问题时,可将有关线段、角度、面积用未知数表示,根据已知条件建立相应的关系式,然后用代数中的恒等变换或解方程得出. 例1 如图1,巳知⊙O的三条弦PP1、QQ1、RR1两两相交,交点分别为A、B、C,且AP=BQ=CR,AR1=BP1=CQ1.求证:△ABC是正三角形.  思路分析 此题用代数法解极为简单. 设BC=x,CA=y,AB=z,AP=BQ=CR=m,AR1=BP1=CQ1=n,由相交弦定理可列出方程组 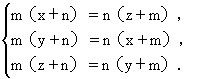 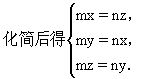 三式相加得m(x+y+z)=n(x+y+z).由m=n可推出x=y=z.所以△ABC是等边三角形. 例2 如图2,已知△AEF是正方形ABCD的内接正三角形,DG⊥DB交BC延长线于G,H在DB上,且DH=DA.求证:GH=GE. 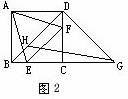 思路分析 本题等量关系虽多,但较杂乱,要证的GH、GE无法从图形上直接找出等量关系.注意到GH可用正方形的边长a来表示,   (责任编辑:admin) |
