|
函数是整个高中阶段乃至高考中的重难点,下面是高中数学给大家带来高一数学新人教A版必修一,第三章3.3幂函数典例精析与方法提炼。  1.幂函数的定义及解析式  方法提炼 型如y=xα(α∈R)的函数是幂函数,xα的系数必须是1,其只有一个参数α,因此只需一个条件即可确定其解析式. 2.幂函数的图象与性质  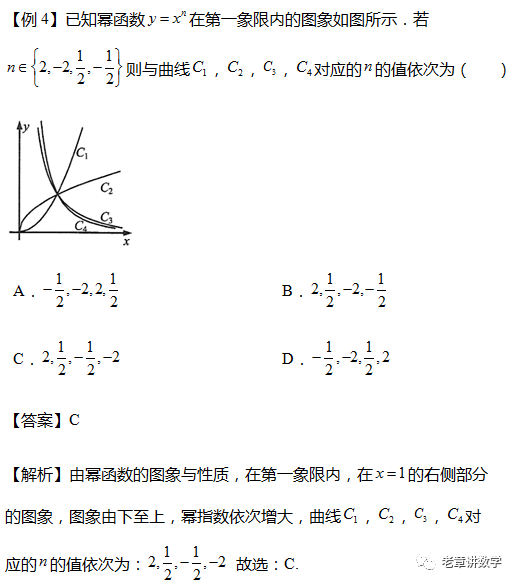      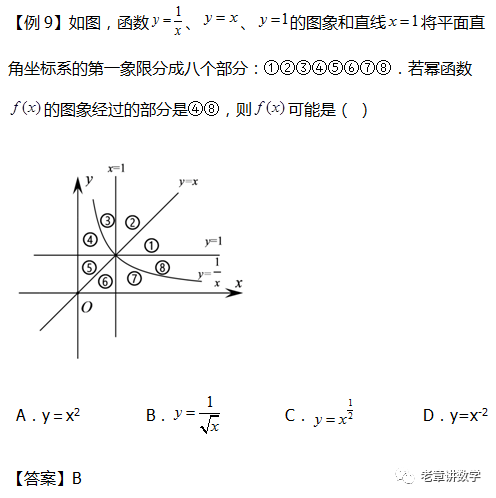      方法提炼 1.幂函数的单调性: ①当α>0时,幂函数的图象都过点(0,0)和(1,1),且在(0,+∞)上单调递增;在第一象限内,当α>1时,图象下凸;当0<α<1时,图象上凸. ②当α<0时,幂函数的图象都过点(1,1),且在(0,+∞)上单调递减. ③在直线x=1的右侧,指数越大,图像越在上方. ④在其他象限的单调性,根据函数的奇偶性,结合图像的对称性进行判断.  2.在比较幂值的大小时,若底数相同常借助指数函数的单调性进行比较;若指数相同常借助幂函数的单调性进行比较;若底数和指数都不相同,常找到一个中间值,通过比较幂函数值与中间值的大小进行判断. 声明: (责任编辑:admin) |
