|
高中数学老师给大家带来新版高二数学必修三,第一章1.3中国古代数学中的算法案例知识点归纳,一起来学习吧。 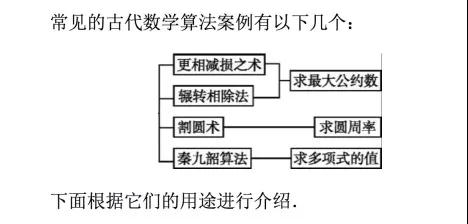 中国古代数学中的算法案例 求两个正整数的最大公约数的算法 更相减损术和辗转相除法都是用来求两个正整数的最大公约数的方法.更相减损术的基本过程是:对于给定的两个数,用较大的数减去较小的数,接着把所得的差与较小的数比较,并以大数减去小数,重复这种操作,直到所得的两数相等为止,所得数即为要求的最大公约数。 程序框图表示为:  辗转相除法的基本过程是:对于给定的两个数,用较大的数除以较小的数所得的余数和较小的数构成新的一对数,重复做上面的除法,直到较大数被较小数除尽,这个较小的数即为要求的最大公约数。 程序框图表示为:  不同点:①更相减损术进行的是减法运算,辗转相除法进行的是除法运算,辗转相除法的计算次数相对更相减损术少.②结果上,更相减损术以减数与差相等而得到最大公约数,辗转相除法则是以相除余数为0得到。 例1 【例1】分别用更相减损术与辗转相除法求261与319的最大公约数. 【解】更相减损术: (261,319)→(261,58)→(203,58)→(145,58)→(87,58)→(29,58)→(29,29). ∴319与261的最大公约数是29. 辗转相除法: 319÷261=1(余58), 261÷58=4(余29), 58÷29=2(余0), ∴319与261的最大公约数是29. 【方法总结】用更相减损术求两个数的最大公约数时,当较大数减较小数的差恰好等于较小数时停止算法,这时的较小数或差即所求的最大公约数.用辗转相除法求两个数的最大公约数时,当较大数除以较小数的余数为零时停止算法,这个较小数即为所求的最大公约数. 例2 【例2】求1356和2400的最小公倍数.  思路分析:两个数的最小公倍数就是这两个数的积与这两个数的最大公约数的商,所以要求1356与2400的最小公倍数,要先求1356与2400的最大公约数。  二割圆术 割圆术是我国魏晋时期的数学家刘徽采用正多边形面积逐渐逼近圆面积的方法计算圆周率π的一种算法.他的思想后来又得到祖冲之的推进和发展。 注意:因为是用圆内接正多边形逼近圆,所以得到的圆周率总是小于π的实际值。 三,秦九韶算法 秦九韶算法是我国宋代数学家秦九韶在他的代表作《数学九章》中提出的一种用于计算多项式的值的方法.直到今天,这种算法仍是世界上多项式求值的最先进的算法。 秦九韶算法适用于形如  例3  2.计算时要由内向外逐次计算,由于下一次计算需要用到上一次的计算结果,故应认真、细心,确保中间结果的准确性。 3.当多项式结构或自变量的值较为简单时,可将自变量的值代入多项式求解或验证。 声明: (责任编辑:admin) |
