|
自由电子能否完全吸收一个光子? ──谈光电效应和康普顿效应的模型问题 江苏南通市第二中学 陈雅 有这样一道习题:1924年法国物理学家德布罗意提出物质波的概念,任何一个运动着的物体,小到电子,大到行星、恒星都有一种波与之对应,波长为λ=h/p,p为物体运动的动量,h为普朗克常数,同样,光也具有粒子性,光子的动量为:p=h/λ,根据上述观点可以证明一个静止的自由电子如果完全吸收一个γ光子,会发生下列情况:设光子的频率为υ,则E=hυ,p=hυ/c,电子吸收光子后,hυ=mev2/2,得v=2c电子的速度为光速的两倍,显然这是不可能的,关于上述过程,下列说法正确的是( ) A.因为微观世界动量守恒定律不适用,上述论证错误,所以电子有可能完全吸收一个γ光子 B.因为微观世界能量守恒定律不适用,上述论证错误,所以电子有可能完全吸收一个γ光子 C.动量守恒定律、能量守恒定律是自然界中普遍适用的规律,所以唯一的结论是电子不可能完全吸收一个γ光子 D.若γ光子与一个静止的自由电子发生作用,则γ光子被电子散射后频率增大 对这个问题,学生可以根据常识“动量守恒定律、能量守恒定律是自然界中普遍适用的规律”从而可判断选项A、B错误,同时学生头脑中有康普顿效应的印象,所以能判断γ光子被电子散射后因能量变小从而频率降低,所以选项D错误,因此选择C。但同时,学生对“电子不可能完全吸收一个光子”存在疑虑,因为他们头脑中有光电效应中金属内部电子在吸收一定能量的光子后克服逸出功从而成为自由电子、以及玻尔能级跃迁中基态的电子吸收一定频率的光子后能跃迁到较高能级的印象,在这两个例子中,都是电子吸收光子的。所以爱思考的同学就在考虑是否题目有误,本题没有一个选项正确。 当然,对自由电子不能完全吸收一个γ光子,可以很简单地用动量守恒定律和能量守恒定律加以推断。 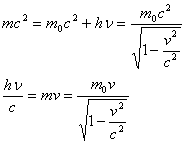 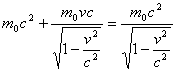 显然,v=0应舍弃,但是如果v=c,由于电子的静止质量不为零,当v=c时,电子的运动质量为无穷,这是不可以的。因此,电子的速度不可能为c(最多是接近光速c,如构成β射线的电子流速度约为0.99c),从而证明自由电子不能完全吸收一个γ光子。因此上题中选项C是正确的。但是题目中所给出的推导过程有误:“电子吸收光子后,hυ=mev2/2,得v=2c”,吸收的能量转化为动能这是正确的,但既然这里讨论的电子的速度很大(其推导结果为v=2c),而增加的动能,这里仍然用经典表达,显然是不合理的。 这样,我们证明了选项C的正确性,那么又如何解决学生头脑中关于“光电效应中电子跃迁吸收光子”与这里“自由电子不能吸收光子──即康普顿效应”之间的“矛盾”呢?下面将讨论这两种效应的不同处理方式。 一般光电效应是在可见光、紫外光的照射下发生的,此时入射光子的能量仅有几个eV(可见光不超过3.2eV),与金属的束缚能量(W)相比较,有相近的数量级,甚至光子能量小于束缚能量,所以不能把电子视为“自由电子”,必须考虑原子对电子对束缚作用,在光电效应的爱因斯坦方程(即能量守恒方程)中,必须有束缚能量项,它包括两部分:一是原子其他部分对价电子的束缚能(电离能或结合能);一是电子逸出物质表面所需的能量(逸出功)。也就是说,电子是束缚电子,与原子其他部分构成束缚系统,光子与整个束缚系统能量守恒。光电效应方程的一般形式为 其中:hυ为入射光子的能量,Ek是被释放的电子动能,A为电子脱离原子的束缚能量(电离能),W为电子逸出物质表面界限的功函数(逸出功)。 对金属来说,由于其内部有大量原子束缚微弱的外层电子,所以可略去束缚能A,方程变为 上式正是一般教材中给出的爱因斯坦光电效应方程。总之,在光电效应中采用束缚电子模型是从能量角度考虑的。 那么,既然在微观过程中动量守恒和能量守恒都是成立的,光电效应中为何只考虑能量守恒?或者说光电效应中动量守恒吗?如前所述,在光电效应中采用的是束缚电子模型,能量守恒系统除了光子和电子外,还有原子和原子核(或离子)等的能量消耗(A和W)。因此对光电效应应用动量守恒的系统除了光子和电子外,也要考虑其它物质的反冲。以氢原子为例,用波长为200 其中Eek为光电子获得的最大初动能,Epk为原子(本例中是质子)的动能。但质子的质量要比电子的质量大很多,所以质子可以看出重靶,根据碰撞理论,重靶动能很小即Epk很小,可以忽略不计。因此⑴变为 而电子的静能 若动量守恒,应为光子、电子及反冲质子三者守恒,则有 可见质子(原子)将以巨大的动量朝着与光电子相反的方向反冲。所以质子在光电相互作用中不仅具有动量且动量很大,因此,在研究光电效应的动量守恒时,不能只谈光子和电子的动量守恒。但是尽管质子的动量如此之大,事实却不是这样。因为在一般情况下(例如在金属中)一个原子或原子核的反冲,将在晶格内所有原子而不是被一个原子或原子核所取得,而晶体含有大量原子。由于晶体的总质量同光电子比较是如此巨大,从而导致反冲动量趋于零,所以实际上观察不到光电效应中的反冲现象。 而在康普顿效应中,电子是处于原子核的束缚之中,所以本质上仍是束缚电子。但是,由于入射光子是X射线,X射线光子能量通常是104—105eV的数量级,而靶物质如石墨、石蜡等散射体(轻元素)中电子的结合能至多只有几十个eV量级,这时两者相差好几个量级。从能量的比较上,电子所受束缚小得可以忽略不计,所以被当作“自由电子”看待。既然是“自由电子”,就可以脱离原子的束缚系统。在与入射光子作用时,就不再考虑整个原子束缚系统,而只考虑光子—电子系统。再微观理论中,看作是光子—电子作弹性碰撞,光子—电子系统能量守恒、动量守恒。 静止电子相碰,碰后光子的能量为hυ,电子的速度为v,光子碰后的运动方向与其原入射方向的夹角为θ,电子碰后飞出的方向与入射光子入射方向的夹角为φ。为了简便,设发生光电效应时电子朝入射光子的方向运动。由动量守恒和能量守恒关系  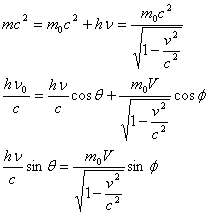 可见,光子散射后波长变长、能量变小。 综上所述,可以看出入射光子的能量大小在决定光电效应和康普顿效应发生的微观模型及其理论解释中所起的重要作用。实际上,正是入射光能量的变化,引起了光子—电子作用机制的变化。在这里“自由”和“束缚”都是相对的。而模型是根据不同的具体物理问题引出来的,因而都只适用于不同的特定的物理过程。 光电效应和康普顿效应只是光子与原子碰撞时,可能会发生的诸多效应中的二种,还可能引起电子偶的产生(光子湮灭,其能量分化为电子和正电子的能量)等效应。在电磁辐射和物质的相互作用中,有时产生光电效应,有时产生康普顿效应(也可产生其它更复杂的现象)。按量子力学理论,我们无法精确地给出这些过程到底哪一个实际会发生,但是我们能给出每一个过程出现的几率。实验表明,对同种靶物质来说,光电效应和康普顿效应发生的几率取决于入射光子的能量。因此我们可以选择某些条件使光电效应成为主要过程或选择其它条件使康普顿效应成为主要过程。而同样是光子和原子的碰撞问题,在不同的效应中采用了不同的模型,作了适当的理想处理,这是为了方便研究的需要,也是物理学处理问题常用的方法。 (责任编辑:admin) |
